Đặt điện áp $\Large\ u=100\sqrt{2}c\text{os100}\pi \text{t(V)}$vào hai

Đặt điện áp $\Large\ u=100\sqrt{2}c\text{os100}\pi \text{t(V)}$vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Thay đổi C để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại; khi đó điện áp hiệu dụng ở hai đầu cuộn cảm là $\Large\ U_L = 97,5$ V. So với điện áp hai đầu đoạn mạch thì điện áp hai đầu điện trở thuần

• A.

  A. sớm pha hơn một góc 0,22π. 

• B.

  B. sớm pha hơn 0,25π.

• C.

  C. trễ pha hơn một góc 0,22π.

• D.

  D. trễ pha hơn một góc 0,25π.

Khi C thay đổi để $\Large\ U_{Cmax}$ Ta có $\Large\ {{\vec{U}}_{RL}}\bot \vec{U}$, biểu diễn trên giản đồ Vecto ta được:

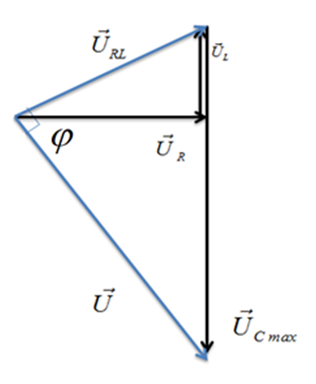
Áp dụng hệ thức lượng trong tam giác vuông ta có :
$\Large\ \dfrac{1}{U_{R}^{2}}=\dfrac{1}{{{U}^{2}}}+\dfrac{1}{U_{RL}^{2}}=>\dfrac{1}{U_{R}^{2}}=\dfrac{1}{{{U}^{2}}}+\dfrac{1}{U_{R}^{2}+U_{L}^{2}}$
$\Large\ \Rightarrow \dfrac{1}{U_{R}^{2}}=\dfrac{1}{{{100}^{2}}}+\dfrac{1}{U_{R}^{2}+{{97,5}^{2}}}$
$\Large\ \Rightarrow {{U}_{R}}=78,06(\Omega )$
Độ lệch pha giữa điện áp hai đầu đoạn mạch và điện áp hai đầu điện trở thuần : $\Large\ \text{cos}\varphi =\dfrac{{{U}_{R}}}{U}=\dfrac{78,06}{100}\Rightarrow \varphi =0,22\pi $
→ Đáp án A