Cho đoạn mạch điện xoay chiều AB gồm điện trở R = 80 $\Large\ \Omega$,

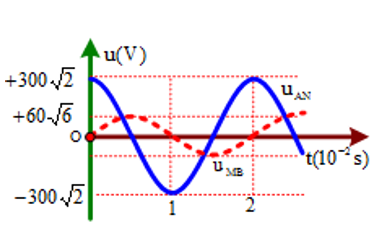
Cho đoạn mạch điện xoay chiều AB gồm điện trở R = 80 $\Large\ \Omega$, cuộn dây không thuần cảm có điện trở r = 20 $\Large\ \Omega$ và tụ điện C mắc nối tiếp. Gọi M là điểm nối giữa điện trở R với cuộn dây, N là điểm nối giữa cuộn dây và tụ điện. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng không đổi U thì điện áp tức thời giữa hai điểm A, N (kí hiệu $\Large\ u_{AN}$ ) và điện áp tức thời giữa hai điểm M, B (kí hiệu $\Large\ u_{MB}$ ) có đồ thị như hình vẽ. Điện áp hiệu dụng U giữa hai đầu đoạn mạch AB có giá trị xấp xỉ bằng

 

 

 

  

• A.

  A. 150$\Large\ \sqrt{2}$ V.

• B.

  B. 225 V.

• C.

  C. 285 V

• D.

  D. 275 V

+ Từ đồ thị ta có: $\Large\ \left\{ \begin{align}   & {{U}_{AN}}=300V \\   & {{U}_{MB}}=60\sqrt{3}V \\  \end{align} \right.$ và $\Large\ u_{AN}$ vuông hpa với $\Large\ u_{MB}$
$\Large\ \Rightarrow {{\cos }^{2}}{{\varphi }_{AN}}+{{\cos }^{2}}{{\varphi }_{MB}}=1\Leftrightarrow {{\left( \dfrac{{{U}_{Rr}}}{{{U}_{AN}}} \right)}^{2}}+{{\left( \dfrac{{{U}_{r}}}{{{U}_{MB}}} \right)}^{2}}=1$ 
$\Large\ \Leftrightarrow {{I}^{2}}\left( \dfrac{20+80}{300} \right)+{{I}^{2}}{{\left( \dfrac{20}{60\sqrt{3}} \right)}^{2}}=1\Rightarrow I=\dfrac{3\sqrt{3}}{2}A$     .
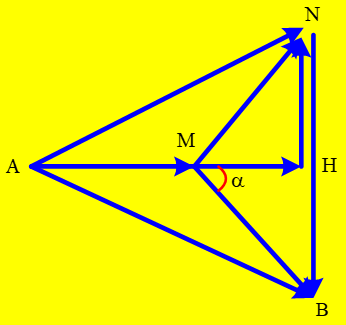
+ Kết hợp với giản đồ véc tơ, với $\Large\ \left\{ \begin{align}   & r=20\Omega  \\   & R=80\Omega  \\  \end{align} \right.$ $\Large\ \Rightarrow \left\{ \begin{align}   & {{U}_{MH}}=30\sqrt{3}V \\   & {{U}_{AM}}=120\sqrt{3} \\  \end{align} \right.$ 
$\Large\ \Rightarrow \alpha ={{60}^{0}}\Rightarrow \angle AMB={{120}^{0}}$ 
+ Vậy $\Large\ {{U}_{AB}}=\sqrt{U_{AM}^{2}+U_{MB}^{2}-2{{U}_{AM}}{{U}_{MB}}\cos {{120}^{0}}}=60\sqrt{21}\sim 275\left( V \right)$ 
→ Đáp án A