Đặt điện áp xoay chiều $\Large\ u=200\sqrt{2}\cos 100\pi t(V)$ vào hai

Đặt điện áp xoay chiều $\Large\ u=200\sqrt{2}\cos 100\pi t(V)$ vào hai đầu đoạn mạch AB gồm đoạn AM nối tiếp đoạn MB thì cường độ hiệu dụng qua mạch là 3A. Điện áp tức thời trên AM và MB lệch pha nhau $\Large\ \pi/2$. Đoạn mạch AM gồm cuộn cảm thuần có cảm kháng $\Large\ 20\sqrt{3}\Omega $ nối tiếp với điện trở thuần 20 $\Large\ \Omega$ và trên đoạn mạch MN là hộp kín X. Hộp X chứa hai trong ba phần tử hoặc điện trở thuần $\Large\ R_0$, hoặc cuộn cảm thuần có cảm kháng $\Large\ Z_{L0}$ hoặc tụ điện có dung kháng $\Large\ Z_{C0}$ mắc nối tiếp. Hộp X chứa

• A.

  A. $\Large\ R_0 = 120 \Omega$ và $\Large\  Z_{C0} = 120 \Omega$ 

• B.

  B. $\Large\ R_0 = 46,2 \Omega$ và $\Large\ Z_{C0} = 26,7 \Omega$

• C.

  C. $\Large\ R_0 = 93,8 \Omega$ và $\Large\ Z_{C0} = 54,2 \Omega$

• D.

  D. $\Large\ R_0 = 120 \Omega$ và $\Large\ Z_{C0} = 54,2 \Omega$

Ta có giản đồ vecto: 

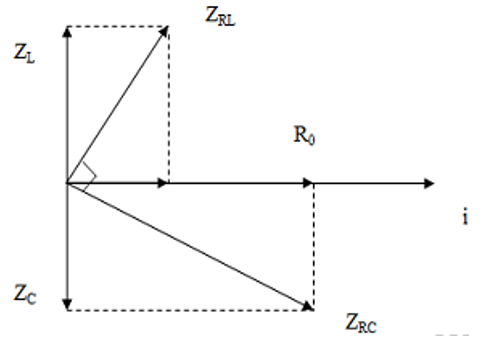
Từ giản đồ vecto ta thấy đoạn mạch MB phải chứa hai phần tử R và C.
Ta có:
$\Large\ {{Z}_{L}}=20\sqrt{3}\Omega ;R=20\Omega .$
$\Large\ \Rightarrow {{\varphi }_{1}}={{60}^{0}}\Rightarrow {{\varphi }_{2}}={{90}^{0}}-{{60}^{0}}={{30}^{0}}$
$\Large\ \tan {{\varphi }_{2}}=\dfrac{-{{Z}_{C}}}{{{R}_{0}}}=\tan {{30}^{0}}\Rightarrow {{R}_{0}}=\sqrt{3}{{Z}_{C}}$
Vì U = 200 V và I = 3 A nên tổng trở Z = 200/3 $\Large\ \Omega$. Ta có :
$\Large\ {{Z}^{2}}={{(R+{{R}_{0}})}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}\Leftrightarrow \dfrac{{{200}^{2}}}{{{3}^{2}}}={{(20+\sqrt{3}{{Z}_{C}})}^{2}}+{{(20\sqrt{3}-{{Z}_{C}})}^{2}}$
$\Large\ \Rightarrow {{Z}_{C}}=\dfrac{80}{3}=26,7\Omega \Rightarrow {{R}_{0}}=46,2\Omega $
→ Đáp án B