Có tất cả bao nhiêu số nguyên $\Large m$ thỏa mãn đồ thị hàm số $\Larg

Có tất cả bao nhiêu số nguyên $\Large m$ thỏa mãn đồ thị hàm số $\Large y=x^3+2020x+m$ và trục hoành có điểm chung?

• A. vô số.
• B. 2020.
• C. 4080.
• D. 2021.

Phương trình hoành độ giao điểm của đồ thị hàm số $\Large y=x^3+2020x+m$ và trục hoành là $\Large x^3+2020x+m=0\Leftrightarrow -x^3-2020x=m$ (*).

Xét hàm số $\Large f(x)=-x^3-2020x$ xác định trên $\Large \mathbb{R}$.

Bảng biến thiên:

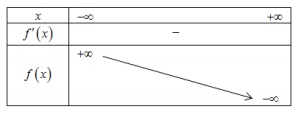
Đồ thị hàm số $\Large y=x^3+2020x+m$ và trục hoành có điểm chung khi và chỉ khi phương trình (*) có nghiệm $\Large \Leftrightarrow$ đồ thị hàm số $\Large f(x)=-x^3-2020x$ và đường thẳng $\Large y=m$ có điểm chung.

Dựa vào bảng biến thiên ta thấy đường thẳng $\Large y=m$ luôn cắt đồ thị hàm số $\Large f(x)=-x^3-2020x$ nên pt (*) luôn có nghiệm với mọi $\Large m$.

Vậy có vô số giá trị nguyên của $\Large m$ thỏa mãn yêu cầu bài toán.