Cho ba số dương $\Large a$, $\Large b$, $\Large c$. Trong không gian t

Cho ba số dương $\Large a$, $\Large b$, $\Large c$. Trong không gian tọa độ $\Large Oxyz$, cho hai điểm $\Large A(a; 0; c)$ và $\Large B(c; a; b)$. Giả sử đường thẳng $\Large AB$ cắt mặt phẳng $\Large (Oxy)$ tại điểm $\Large I$. Tỉ số $\Large \dfrac{IA}{IB}$ bằng

• A.

  $\Large \dfrac{b}{c}$.

• B.

  $\Large \dfrac{b}{c}$.

• C.

  $\Large \dfrac{c}{b}$.

• D.

  $\Large \dfrac{a}{c}$.

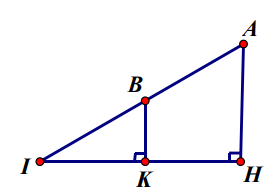
Do $\Large b$, $\Large c$ dương nên $\Large A(a; 0; c)$ và $\Large B(c; a; b)$ cùng phía mặt phẳng $\Large (Oxy)$.

Gọi $\Large H$ là hình chiếu của $\Large A(a; 0; c)$ lên mặt phẳng $\Large (Oxy)$ là: $\Large H(a; 0; 0)$.

Gọi $\Large K$ là hình chiếu của $\Large B(c; a; b)$ lên mặt phẳng $\Large (Oxy)$ là: $\Large K(c; a; 0)$.

Ta có: $\Large \overrightarrow{AH}=(0; 0; -c)\Rightarrow AH=|c|=c$ (vì $\Large c > 0$) và $\Large \overrightarrow{BK}=(0; 0; -b)\Rightarrow BK=|b|=b$ (vì $\Large b > 0$).

Vì $\Large BK// AH$ nên $\Large \dfrac{IA}{IB}=\dfrac{AH}{BK}=\dfrac{c}{b}$.

Vậy $\Large \dfrac{IA}{IB}=\dfrac{c}{b}$.