Có nhiều nhất bao nhiêu số nguyên thuộc khoảng nghịch biến của hàm số

Có nhiều nhất bao nhiêu số nguyên thuộc khoảng nghịch biến của hàm số $\large y=\dfrac{1}{3} x^{3}-x^{2}-3 x+1 ?$

• A.

  A. vô số

• B.

  B. 2

• C.

  C. 3

• D.

  D. 5

Tập xác định: $\large D=\mathbb{R}$

Ta có $\large y^{\prime}=x^{2}-2 x-3 ; y^{\prime}=0 \Leftrightarrow x^{2}-2 x-3=0 \Leftrightarrow\left[\begin{array}{l}
x=-1 \\
x=3
\end{array}\right.$

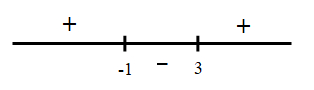
Suy ra hàm số nghịch biến trên khoảng (-1;3).

Trong khoảng (-1;3) có 3 số nguyên là:{ 0; 1; 2} $\large \Rightarrow$ đáp án C.