Chướng ngại vật “ tường cong ” trong một sân thi đấu X - Game là một k

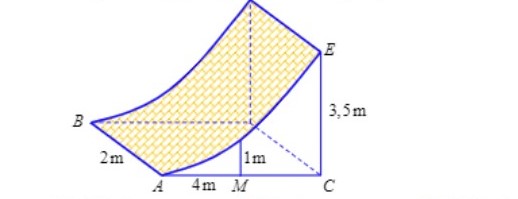
Chướng ngại vật “ tường cong ” trong một sân thi đấu X - Game là một khối bê tông có chiều cao từ mặt đất lên là 3,5m . Giao của mặt tường cong và mặt đất là đoạn thẳng AB = 2m . Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với AB tại A là một hình tam giác vuông cong ACE với AC = 4m , CE = 3,5m và cạnh cong AE nằm trên một đường parabol có trục đối xứng vuông góc với mặt đất . Tại vị trí M là trung điểm của AC thì tường cong có độ cao 1m ( xem hình minh họa bên ) . Tính thể tích bê tông cần sử dụng để tạo nên khối tường cong đó .

• A.

  $\Large 9,75{{m}^{3}}$

• B.

  $\Large 10,5{{m}^{3}}$

• C.

  $\Large 10{{m}^{3}}$

• D.

  $\Large 10,25{{m}^{3}}$

Chọn C

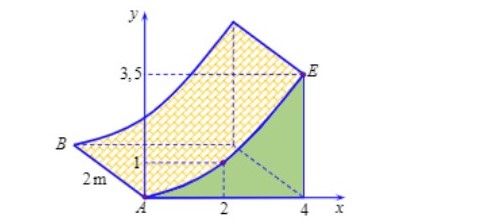
Chọn hệ trục $\Large Oxy$ như hình vẽ sao cho $\Large A\equiv O$ 

$\Large \Rightarrow$ cạnh cong AE nằm trên parabol $\Large (P)$: $\Large y=a{{x}^{2}}+bx$ đi qua các điểm (2;1) và $\Large \left( 4;\dfrac{7}{2} \right)$ nên $\Large (P)$: $\Large y=\dfrac{3}{16}{{x}^{2}}+\dfrac{1}{8}x$

Khi đó diện tích tam giác cong ACE có diện tích $\Large S=\int\limits_{0}^{4}{\left( \dfrac{3}{16}{{x}^{2}}+\dfrac{1}{8}x \right)dx=5{{m}^{2}}}$

Thể tích khối bê tông cần sử dụng để tạo nên khối tường cong đó là $\Large V=S.h=5.2=10m^3$