Cho tứ diện $\large ABCD$ có $\large AB=CD=2a$. Gọi $\large M,N$ lần l

Cho tứ diện $\large ABCD$ có $\large AB=CD=2a$. Gọi $\large M,N$ lần lượt là trung điểm của $\large BC,AD$ và $MN=a\sqrt{3}$. Tính góc tạo bởi hai đường thẳng $\large AB$ và $\large CD$.

• A.

  A. $\large 30^{\circ}$

• B.

  B. $\large 45^{\circ}$

• C.

  C. $\large 60^{\circ}$

• D.

  D. $\large 90^{\circ}$

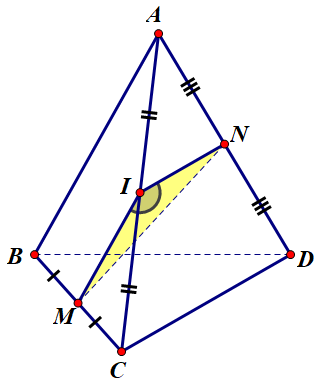
Gọi $\large I$ là trung điểm của $\large AC$, suy ra:

$\large\left\{\begin{align}MI//AB;NI//CD\\ MI=NI=a\end{align}\right.$

Khi đó $\large (\widehat{AB,CD})=(\widehat{MI,NI})$.

Xét tam giác $\large MIN$ ta có:

$\large\cos \widehat{MIN}=\frac{MI^{2}+NI^{2}-MN^{2}}{2MI.NI}=\frac{2a^{2}-3a^{2}}{2a^{2}}=-\frac{1}{2}\Rightarrow \widehat{MIN}=120^{\circ}$

Suy ra $\large (\widehat{MI,NI})=60^{\circ}$ hay $\large (\widehat{AB,CD})=60^{\circ}$