Cho tứ diện ABCDABCD có các cạnh AB=BC=CD=DA=1AB=BC=CD=DA=1 và $\larg
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho tứ diện ABCDABCD có các cạnh AB=BC=CD=DA=1AB=BC=CD=DA=1 và AC,BDAC,BD thay đổi. Thể tích ABCDABCD đạt giá trị lớn nhất bằng:
Đáp án án đúng là: B
Lời giải chi tiết:
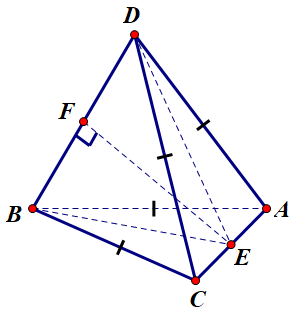
Đặt AC=x,BD=y(x,y>0)AC=x,BD=y(x,y>0)
Gọi E,FE,F lần lượt là trung điểm AC,BDAC,BD
△ABC=△ADC(c.c.c)⇒DE=BE⇒EF⊥BD△ABC=△ADC(c.c.c)⇒DE=BE⇒EF⊥BD. Chứng minh tương tự EF⊥ACEF⊥AC
Suy ra EFEF là đoạn vuông góc chung của AC,BDAC,BD
Ta có {AC⊥EFAC⊥BE ⇒AC⊥(BED)
VABCD=2VABDE=213AE.S△BED=23AE.EF.BF=23⋅x2⋅y2⋅EF (1)
Trong △BEF:EF2=BE2−BF2=1−x24−y24.
Ta có:
V2ABCD=1144⋅x2⋅y2⋅(4−x2−y2)≤1144(x2+y2+(4−x2−y2)3)3=4243⇔maxVABCD=2√327
Dấu "=" xảy ra khi x2=y2=4−x2−y2⇔x=y=2√327
Đáp án B
Xem thêm các bài tiếp theo bên dưới