Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích

Cho hình chóp $\large S.ABCD$ có đáy là hình bình hành và có thể tích là $\large V$. Gọi $\large P$ là điểm trên cạnh $\large SC$ sao cho $\large SC=5SP$. Một mặt phẳng $\large (\alpha )$ qua $\large AP$ cắt hai cạnh $\large SB,SD$ lần lượt tại $\large M,N$. Gọi $\large V_{1}$ là thể tích của khối chóp $\large S.AMPN$. Tìm giá trị lớn nhất của $\large\frac{V_{1}}{V}$

• A.

  A. $\large\frac{2}{15}$

• B.

  B. $\large\frac{1}{15}$

• C.

  C. $\large\frac{1}{25}$

• D.

  D.$\large\frac{3}{25}$

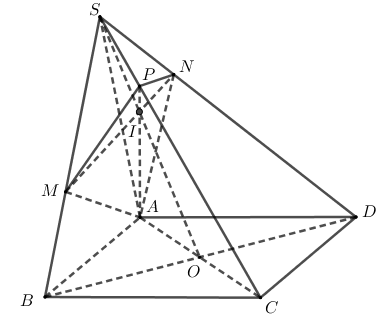
Cách 1.

Ta có: $\large\frac{V_{1}}{V}=\frac{V_{S.AMPN}}{V_{S.ABCD}}=\frac{V_{S.APN}+V_{S.APM}}{2V_{S.ABC}}=\frac{1}{2}\left ( \frac{SP}{SC}\cdot \frac{SN}{SD}+\frac{SP}{SC}\cdot \frac{SM}{SB} \right )=\frac{1}{10}\left ( \frac{SN}{SD}+\frac{SM}{SB} \right )$. Đặt $\large a=\frac{SM}{SB},b=\frac{SN}{SD},0< a,b\leq 1$

Gọi $\large O$ là giao điểm hai đường chéo của hình bình hành $\large ABCD$

Trong mặt phẳng $\large (SAC),AP\cap SO=I$

Xét tam giác $\large SOC$ có $\large\frac{PS}{PC}\cdot \frac{AC}{AO}\cdot \frac{IO}{IS}=1\Leftrightarrow \frac{IO}{SO}=2\Rightarrow \frac{SI}{SO}=\frac{1}{3}$

Xét tam giác $\large SBD$ có $\large\frac{S_{SMN}}{S_{SBD}}=\frac{SM}{SB}\cdot \frac{SN}{SD}=ab$

Mặt khác, $\large\frac{S_{SMN}}{S_{SBD}}=\frac{S_{SMI}+S_{SNI}}{S_{SBD}}=\frac{S_{SMI}}{2S_{SBO}}+\frac{S_{SNI}}{2S_{SDO}}=\frac{1}{2}\left ( \frac{SM}{SB}\cdot \frac{SI}{SO}+\frac{SN}{SD}\cdot \frac{SI}{SO} \right )=\frac{1}{6}(a+b)$

Vậy, $\large\frac{1}{6}(a+b)=ab$ do $\large a=\frac{1}{6}$ không thỏa mãn hệ thức nên $\large b=\frac{a}{6a-1}$, do $\large 0< b\leq 1$ nên $\large 0< \frac{a}{6a-1}\leq 1\Leftrightarrow a\geq \frac{1}{5}$. Từ đó, $\large\frac{V_{1}}{V}=\frac{1}{10}(a+b)=\frac{1}{10}\left ( a+\frac{a}{6a-a} \right )$ với $\large\frac{1}{5}\leq a\leq 1$

Xét hàm số $\large y=f(x)=x+\frac{x}{6x-1}$ với $\large x\epsilon \left [ \frac{1}{5};1 \right ].{y}'=1-\frac{1}{(6x-1)^{2}}$,

$\large {y}'=0\Leftrightarrow (6x-1)^{2}=1\Leftrightarrow \left [\begin{align}x=0(L)\\ x=\frac{1}{3}\end{align}\right.$. Ta có $\large f(\frac{1}{5})=\frac{6}{5},f(\frac{1}{3})=\frac{2}{3},f(1)=\frac{6}{5}$. Vậy $\large\underset{x\epsilon \left [ \frac{1}{5},1 \right ]}{max}f(x)=f(1)=\frac{6}{5}$

Từ đó giá trị lớn nhất của $\large\frac{V_{1}}{V}=\frac{3}{25}$ khi $\large M\equiv B$ hoặc $\large N\equiv D$

Cách 2.

* Đặt $\large a=\frac{SA}{SA}=1;b=\frac{SB}{SM};c=\frac{SC}{SP}=5;d=\frac{SD}{SN}$

* Ta có $\large a+c=b+d\Leftrightarrow 1+5=b+d\Leftrightarrow d=6-b$

* $\large\frac{V_{S.AMPN}}{V_{S.ABCD}}=\frac{a+b+c+d}{4abcd}=\frac{1+b+5+6-b}{4\cdot 1\cdot b\cdot 5\cdot (6-b)}=\frac{3}{5}\cdot \frac{1}{-b^{2}+6b}$

* Xét $\large f(b)=\frac{3}{5}\cdot \frac{1}{-b^{2}+6b};b\epsilon \left [ 1;5 \right ](do\quad b,d\geq 1)$

$\large {f}'(b)=-\frac{3}{5}\cdot \frac{-2b+6}{(-b^{2}+6b)^{2}};{f}'(b)=0\Leftrightarrow b=3$

Bảng biến thiên:

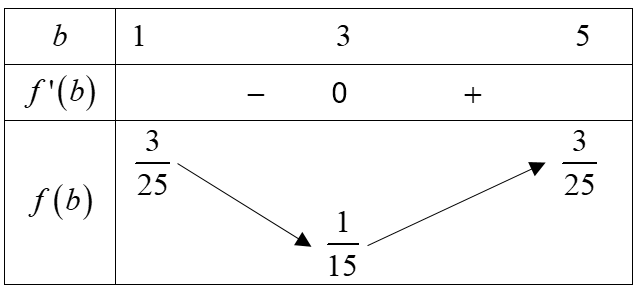
Kết luận: Giá trị lớn nhất của $\large\frac{V_{1}}{V}=\frac{3}{25}$

Đáp án D