Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh bằng 1, SO vuông góc với mặt đáy (ABCD) và SC=1. Thể tích lớn nhất của khối chóp bằng:
Đáp án án đúng là: D
Lời giải chi tiết:
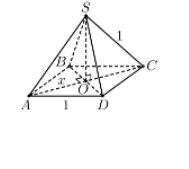
Đặt OA=OC=x. Suy ra OD=√1−x2, SO=√1−x2.
Điều kiện: $\large 0
Thể tích khối chóp
VS.ABCD=13SABCD.SO=13⋅2x√1−x2⋅√1−x2=23x(1−x2)
Xét hàm f(x)=x(1−x2) trên (0,1), ta được
max(0,1)f(x)=f(1√3)=23√3
Vậy thể tích lớn nhất của khối chóp bằng 4√327
Đáp án D
Xem thêm các bài tiếp theo bên dưới