Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. C
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Các mặt bên (SAB),(SAC) lần lượt tạo với mặt đáy các góc là 60∘,30∘. Hình chiếu vuông góc của S trên mặt phẳng đáy nằm trên cạnh BC. Thể tích của khối chóp đã cho bằng:
Đáp án án đúng là: C
Lời giải chi tiết:
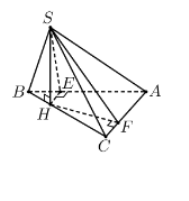
Kẻ HE⊥AB(EϵAB),HF⊥AC(FϵAC) (tham khảo hình vẽ).
Từ hình vẽ, suy ra {^SEH=60∘^SFH=30∘ →{HE=SH.cot60∘HF=SH.cot30∘
Ta có S△ABH+S△ACH=S△ABC⇔12AB.HE+12AC.HF=a2√34
⇔12.a.SH.(cot60∘+cot30∘)=a2√34→SH=3a8
Vậy thể tích khối chóp: VS.ABC=13S△ABC.SH=a3√332
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cậ
- Cho hình chóp S.ABC có $\large SB=a, SC=2a, \widehat{BSC}=60^
- Cho hình chóp S.ABCcó đáy ABC là tam giác vuông cân
- Cho hình chóp đều S.ABCD đáy tâm O và có cạnh bằng $
- Hình đa diện nào dưới đây không có tâm đối xứng? A. Tứ diện đều B. Bát