Cho tứ diện $\large ABCD$ có hình chiếu của $\large A$ lên mặt phẳng $

Cho tứ diện $\large ABCD$ có hình chiếu của $\large A$ lên mặt phẳng $\large (BCD)$ là $\large H$ nằm trong tam giác $\large BCD$. Biết rằng $\large H$ cũng là tâm của một mặt bán kính $\large\sqrt{3}$ và tiếp xúc các cạnh $\large AB,AC,AD$. Dựng hình bình hành $\large ABHS$. Tính giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp hình chóp $\large S.BCD$

• A.

  A. 3

• B.

  B. $\large 3\sqrt{3}$

• C.

  C. $\large\frac{3}{2}$

• D.

  D. $\large\frac{3\sqrt{3}}{2}$

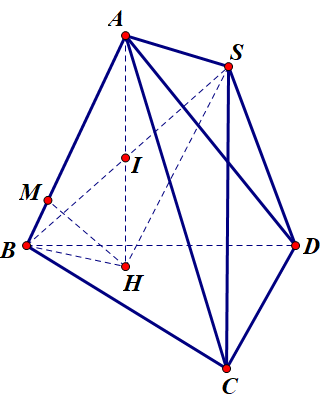
Gọi $\large M,N,P$ lần lượt là hình chiếu của $\large H$ lên $\large AB,AC,AD$ ta có

$\large HM=HN=HP=\sqrt{3}\Rightarrow AM=AN=AP\Rightarrow AH\perp (MNP)\Rightarrow (MNP)//(BCD)\Rightarrow AB=AC=AD$ ($\large AH$ là trục đường tròn $\large\bigtriangleup MNP$)

Vậy $\large A$ thuộc trục đường tròn ngoại tiếp $\large\bigtriangleup BCD$

$\large AH$ là trục đường tròn ngoại tiếp $\large \bigtriangleup BCD$

Gọi $\large I=AH\cap BS\Rightarrow IB=IC=ID=IS$. Vậy I là tâm mặt cầu ngoại tiếp $\large S.BCD$

$\large IH=x\Rightarrow \frac{1}{HM^{2}}=\frac{1}{HB^{2}}+\frac{1}{HA^{2}}\Rightarrow HB^{2}=\frac{12x^{2}}{4x^{2}-3}$

$\large\bigtriangleup HBI$ vuông tại $\large H$: $\large BI^{2}=HB^{2}+HI^{2}=\frac{4x^{4}+9x^{2}}{4x^{2}-3}$

$\large t=x^{2}\Rightarrow f(t)=\frac{4t^{2}+9t}{4t-3}(t> \frac{3}{4})\Rightarrow {f}'(t)=\frac{16t^{2}-24t-27}{(4t-3)^{2}}$

$\large {f}'(t)=0\Rightarrow t=\frac{9}{4}(tm)$ hoặc $\large t=-\frac{3}{4}(l)$

Vẽ bảng biến thiên $\large R_{min}=\frac{3\sqrt{3}}{2}$

Đáp án D