Cho tứ diện gần đều ABCD, biết $\large AB=CD=5,\, AC=BD=\sqrt{34},\, A

Cho tứ diện gần đều ABCD, biết $\large AB=CD=5,\, AC=BD=\sqrt{34},\, AD=BC=\sqrt{41}$. Tính $\large \sin$ góc giữa hai đường thẳng AB và CD

• A. A. $\large \dfrac{24}{25}$
• B. B. $\large \dfrac{7}{25}$
• C. C. $\large \dfrac{\sqrt{3}}{2}$
• D. D. $\large \dfrac{1}{3}$

Chọn A

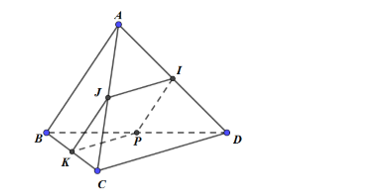
Gọi I, J, K, p lần lượt là trung điểm của AD, AC, BC, BD
Khi đó: $\large AB//IP//IK,\, CD//IJ//KP$
Ta có: $\large \Rightarrow  \angle (AB, CD)= \angle (IP, KP)$
$\large \dfrac{KP}= \dfrac{1}{2}CD= \dfrac{5}{2};\, IP= \dfrac{1}{2}AB= \dfrac{5}{2}$
$\large AK^2= \dfrac{AB^2+AC^2}{2}- \dfrac{BC^2}{4}= \dfrac{25+34}{2}- \dfrac{41}{4}= \dfrac{77}{4}= DK^2$  
Tam giác AKD cân tại K, KI là trung tuyến
$\large \Rightarrow  KI\perp AD\Rightarrow  IK^2= AK^2-AI^2=\dfrac{77}{4}- \dfrac{41}{4}=9$
$\large \cos\widehat{IPK}= \dfrac{IP^2+KP^2-IK^2}{2.IP.KP}= \dfrac{\dfrac{25}{4}+\dfrac{25}{4}-9}{2.\dfrac{5}{2}.\dfrac{5}{2}}= \dfrac{7}{25} > 0 \Rightarrow  \widehat{IPK} < 90^\circ $
$\large \Rightarrow  \angle (AB, CD)= \angle(IP, KP)= \angle IPK\Rightarrow \sin\widehat{(AB, CD)}= \sin\widehat{IPK}= \sqrt{1-\left(\dfrac{7}{25} \right)^2}= \dfrac{24}{25}$