Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết $\large AB=2a,\, AD

Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết $\large AB=2a,\, AD=a,\, SA+3a$ và SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách giữa hai đường thẳng SC và BM bằng

• A. A. $\large \dfrac{3a\sqrt{3}}{4}$
• B. B. $\large \dfrac{2a\sqrt{3}}{3}$
• C. C. $\large \dfrac{a\sqrt{3}}{3}$
• D. D. $\large \dfrac{a\sqrt{3}}{2}$

Chọn C

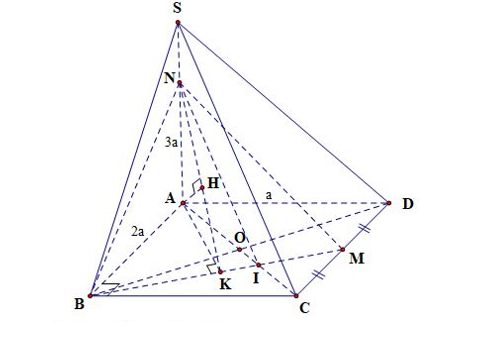
Gọi O là tâm hình chữ nhật, $\large I = BM\cap AC$
Dựng $\large IN//SC\, (N\in SA),\, AK\perp BM,\, AH\perp NK\, (K\in BM,\, H\in NK)$
Dễ CM được $\large AH\perp (BMN)$. Khi đó: 
$\large d(SC, BM) = d(SC, (BMN))= d(C, (BMN))$
Lại có: $\large \dfrac{d(C, (BMN))}{d(A, (BMN))}= \dfrac{CI}{AI}= \dfrac{\dfrac{2}{3}CO}{CO+ \dfrac{1}{3}CO}= \dfrac{1}{2}\Rightarrow  d(C, (BMN))= \dfrac{1}{2}d(A, (BMN))= \dfrac{1}{2}AH$
Xét tam giác vuông ANK: 
$\large AK= \dfrac{2.S_{ABM}}{BM}= \dfrac{2a.a}{\sqrt{a^2+a^2}}= a\sqrt{2}$
$\large \dfrac{AN}{AS}= \dfrac{AI}{AC}= \dfrac{2}{3}\Rightarrow  AN= \dfrac{2}{3}AS= \dfrac{2}{3}.3a= 2a$
Suy ra: $\large AH= \dfrac{AN.AK}{\sqrt{AN^2+ AK^2}}= \dfrac{2a.a\sqrt{2}}{\sqrt{(2a)^2+\left( a\sqrt{2}\right)^2}}= \dfrac{2a\sqrt{3}}{3}$
Vậy $\large d(SC, BM) = \dfrac{1}{2}AH= \dfrac{a\sqrt{3}}{3}$
Đối với lớp 12 có thể sử dụng phương pháp tọa độ như sau: 
Đặt hệ trục tọa độ như hình vẽ, chọn $\large a= 1$. Khi đó ta có: 
$\large A(0; 0; 0),\, B(2; 0; 0),\, C(2; 1; 0),\, D(0; 1; 0),\, S(0; 0; 3)$
M là trung điểm cạnh CD $\large \Rightarrow  M(1; 1; 0)$
Ta có: $\large \overrightarrow{SC}= (-2; -1; 3);\, \overrightarrow{BM}= (-1; 1; 0);\, \overrightarrow(SB)= (2; 0; -3)$
$\large \Rightarrow  \left[ \overrightarrow{SC}; \overrightarrow{BM}\right]= (-3; -3; -3)$
$\large \Rightarrow  d(SC, BM) = \dfrac{\left|\left[\overrightarrow{SC};\overrightarrow{BM}\right]. \overrightarrow{SB} \right| }{\left|\left[ \overrightarrow{SC}; \overrightarrow{BM}\right] \right|}= \dfrac{\left| -3.2-3.0+(-3).(-3)\right|}{\sqrt{(-3)^2+ (-3)^2+ (-3)^2}}= \dfrac{3}{3\sqrt{3}} = \dfrac{\sqrt{3}}{3}$