Cho tứ diện ABCD có thể tích là V. Gọi M, N, P, Q, R lần lượt là trung

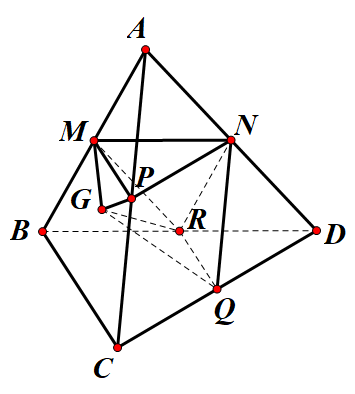
Cho tứ diện ABCD có thể tích là V. Gọi M, N, P, Q, R lần lượt là trung điểm các cạnh AB, AD, AC, DC, BD và G là trọng tâm tam giác ABC (như hình vẽ). Tính thể tích khối đa diện lồi MNPQRG theo V.

• A. A. $\Large \dfrac{V}{3}$
• B. B. $\Large \dfrac{2V}{5}$
• C. C. $\Large \dfrac{V}{6}$
• D. D. $\Large  \dfrac{V}{2}$

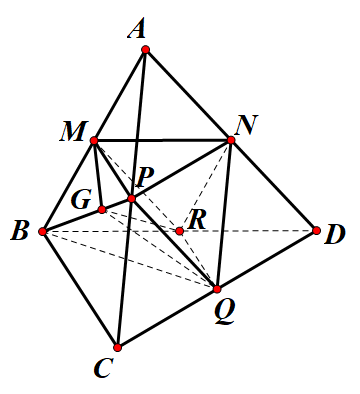
Ta có: $\Large V_{MNPQRG} = V_{G. MPQR} + V_{N.MPQR}$

$\Large \cdot V_{G.MPQR} = \dfrac{1}{3}V_{B.MNQR}$ (do G là trọng tâm tam giác ABC nên $\Large  GP = \dfrac{1}{3}BP$)

$\Large  = \dfrac{2}{3} V_{B.PQR} = \dfrac{2}{3}V_{P.BQR} = \dfrac{2}{3}.\dfrac{1}{2} V_{A.BQR} = \dfrac{1}{3}.\dfrac{1}{4}V_{ABCD} = \dfrac{1}{12}V$

$\Large \cdot V_{N.MPQR} = 2V_{N.MPR} = 2V_{P.MNR} = 2.\dfrac{1}{2}V_{C.MNR} = \dfrac{1}{4}V_{C.ABD} = \dfrac{1}{4}V$

Vậy $\Large V_{MNPQRG} = V_{G.MNQP} + V_{N.MPQR} = \dfrac{1}{12} V + \dfrac{1}{4}V = \dfrac{1}{3}V$