Cho hình lăng trụ đứng $\Large ABC.A'B'C'$ có $\Large AB = a; AC = 2a;

Cho hình lăng trụ đứng $\Large ABC.A'B'C'$ có $\Large AB = a; AC = 2a; \widehat{BAC} = 120^{\circ}$. Gọi M là trung điểm của cạnh $\Large CC'$ thì $\Large \widehat{BMA'} = 90^{\circ}.$ Tính khoảng cách từ điểm A đến mặt phẳng $\Large (BMA')$

• A. A. $\Large  \dfrac{a\sqrt{5}}{7}$
• B. B. $\Large  \dfrac{a\sqrt{5}}{5}$
• C. C. $\Large  \dfrac{a\sqrt{7}}{7}$
• D. D. $\Large  \dfrac{a\sqrt{5}}{3}$

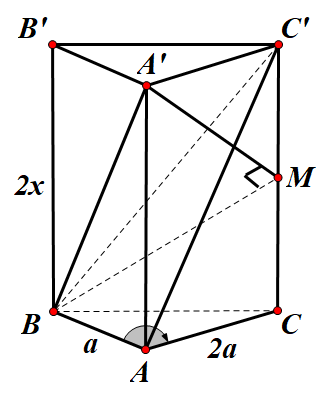
Trong tam giác $\Large BAC$ có $\Large BC^{2} = a^{2} + (2a)^{2} - 2.a.2a.cos120^{\circ} = 7a^{2} \Rightarrow BC = a\sqrt{7}$

Đặt $\Large BB' = 2x \Rightarrow A'B = \sqrt{a^{2} + 4x^{2}} ; A'M = \sqrt{4a^{2} + x^{2}}; BM = \sqrt{7a^{2} + x^{2}}$

Do $\Large \widehat{BMA'} = 90^{\circ} \Rightarrow 4a^{2} + x^{2} + 7a^{2} + x^{2} = a^{2} + 4x^{2} \Rightarrow 2x^{2} = 10a^{2} \Rightarrow x = a\sqrt{5} \Rightarrow h = 2a\sqrt{5}$

Theo định lý Talet $\Large A'A = 2C'M \Rightarrow d(A,(BMA')) = 2.d(C',(BMA')) = 2d$

Ta có $\Large V_{B.B'C'A'} = \dfrac{V}{3} \Rightarrow V_{B.A'C'CA} = \dfrac{2V}{3}$

Lại có $\Large V_{B. C'MA'} = V_{C'.BMA'} = \dfrac{1}{3}.d.S_{BMA'} = \dfrac{1}{3}.d.\dfrac{1}{2} MA'.MB = d.\dfrac{1}{6}.3a.2a\sqrt{3} = d a^{2}\sqrt{3}$

So sánh diện tích $\Large S_{C'MA'} = \dfrac{1}{4} S_{A'C'CA} \Rightarrow V_{B.C'MA'} = \dfrac{1}{4} V_{B.A'C'CA} = \dfrac{1}{4}.\dfrac{2V}{3} = \dfrac{1}{4}.\dfrac{2}{3}a^{3}\sqrt{15} = \dfrac{a^{3}\sqrt{15}}{6}$

Thành thử $\Large  da^{2} \sqrt{3} = \dfrac{a^{3}\sqrt{15}}{6} \Rightarrow d = \dfrac{a\sqrt{5}}{6} \Rightarrow d(A,(BMA')) = 2d = \dfrac{a\sqrt{5}}{3}$