Cho phương trình $\Large m\ln^2(x+1)-(x+2-m)\ln (x+1)-x-2=0 (1).$ Tập

Cho phương trình $\Large m\ln^2(x+1)-(x+2-m)\ln (x+1)-x-2=0 (1).$ Tập tất cả giá trị của tham số $\Large m$ để phương trình $\Large (1)$ có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn $\Large 0 < x_{1} < 2 < 4 < x_{2}$ là khoảng $\Large (a; +\infty)$. Khi đó $\Large a$ thuộc khoảng ?

 

• A.

  A. $\Large (3,8; 3,9)$

• B.

  B. $\Large (3,7; 3,8)$

• C.

  C. $\Large (3,6; 3,7)$

• D.

  D. $\Large (3,5; 3,6)$

Chọn B

Điều kiện xác định: $\Large x>-1$. ta có: 

$\Large m\ln^2 (x+1)-(x+2-m)\ln (x+1)-x-2=0 $

$\Large \Leftrightarrow m\ln^2 (x+1)-(x+2)\ln (x+1)+m\ln (x+1)-(x+2)=0$ 

$\Large \Leftrightarrow m\ln (x+1)[\ln (x+1)+1]-(x+2)[\ln (x+1)+1]=0$ 

$\Large \Leftrightarrow [\ln (x+1)+1][m\ln (x+1)-x-2]=0$ 

$\Large \Leftrightarrow \left[\begin{align}&\ln (x+1)+1=0\\&m\ln (x+1)-x-2=0\\\end{align}\right.$ $\Large \Leftrightarrow\left[\begin{align}&x=e^{-1}-1<0\, (\text{loại})\\&m\ln (x+1)-x-2=0 (*)\\\end{align}\right.$ 

Với $\Large m=0$ thì phương trình (*) có nghiệm $\Large x=-2<0$ (loại) nên không thỏa mãn bài toán 

Với $\Large m\neq 0$ thì $\Large (*)\Leftrightarrow \dfrac{\ln (x+1)}{x+2}=\dfrac{1}{m}$

Xét hàm số $\Large f(x)=\dfrac{\ln (x+1)}{x+2}$ có $\Large f'(x)=\dfrac{\dfrac{x+2}{x+1}-\ln (x+1)}{(x+2)^2}$

Xét hàm số $\Large g(x)=\dfrac{x+2}{x+1}-\ln (x+1)$ có $\Large g'(x)=\dfrac{-1}{(x+1)^2}-\dfrac{1}{x+1}<0, \forall x>-1$

Do đó hàm số $\Large g(x)$ nghịch biến trên khoảng $\Large (-1; +\infty)$

Ta có: $\Large g(2)>0$ và $\Large g(3)<0$ nên $\Large f'(x)=0 \Leftrightarrow g(x)=0 \Leftrightarrow x=x_{0}\in (2; 3)$

$\Large \underset{x\rightarrow +\infty}{lim} f(x)=\underset{x\rightarrow +\infty}{\lim}\dfrac{\ln (x+1)}{x+2}=-\infty$ nên ta có bảng biến thiên trên $\Large (-1; +\infty)$ như sau:

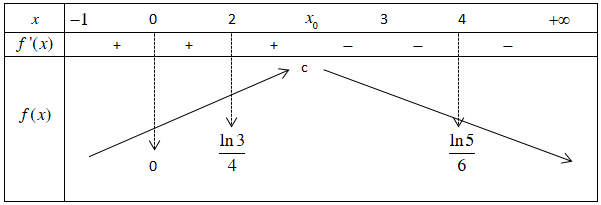
Để phương trình có nghiệm $\Large x_{1}, x_{2}$ thỏa mãn $\Large 0\dfrac{6}{\ln 5}\approx 3, 728$

Suy ra $\Large a\in (3,7; 3,8)$