Cho lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng a, góc gi
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng a, góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60∘60∘. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho
Đáp án án đúng là: A
Lời giải chi tiết:
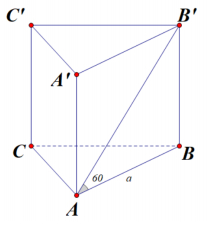
Ta có: (^AB′;(ABC))=(^AB′;AB)=^BAB′=60∘
tan^BAB′=BB′AB ⇒BB′=AB⋅tan^BAB′=a⋅tan60∘=a√3
Bán kính đường tròn ngoại tiếp đáy lăng trụ:R=a√33
⇒V=S⋅h=π(a√33)2⋅a√3=πa3√33
Xem thêm các bài tiếp theo bên dưới
- Cho a=log25,b=log29. Biểu diễn của $\Large P=\lo
- Tính thể tích vật thể giới hạn bởi các mặt phẳng x=0 và $\La
- Tất cả các giá trị của m để hàm số $\Large y=\dfrac{2 \cos x-1}{\cos x
- Cho hàm số y=f(x) có đồ thị như sau Số nghiệm thực của phương
- COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới virus coro