Cho lăng trụ đứng ABC.A′B′C′, đáy là tam giác ABC vu
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ đứng ABC.A′B′C′, đáy là tam giác ABC vuông tại B; AB=2a;BB′=2a√3. Góc giữa A′B và (BCC′B′) bằng
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
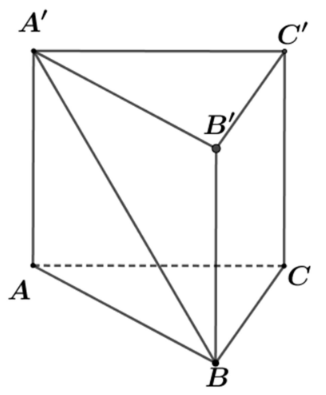
Ta có A′B∩(BCC′B′)=B.
A′B′⊥B′C′;A′B′⊥BB′⇒A′B′⊥(BCC′B′) tại B′
⇒(A′B;(BCC′B′))=(A′B;BB′)=^A′BB′.
Xét ΔA′BB′ vuông ở B′:
tan^A′BB′=A′B′BB′=2a2a√3=1√3⇒^A′BB′=30∘.
Xem thêm các bài tiếp theo bên dưới