Cho khối lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiế

Cho khối lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu của điểm A' trên mặt (ABC) là trung điểm của AB. Biết rằng góc giữa đường thẳng CC' và mặt đáy bằng $\large 60^\circ$. Tính thể tích của khối chóp ACC'B' theo a

• A.

  $\large \dfrac{3a^3}{8}$

   
• B.

  $\large \dfrac{a^3}{4}$

• C.

  $\large \dfrac{3a^3}{4}$

• D.

  $\large \dfrac{a^3}{8}$

Chọn D

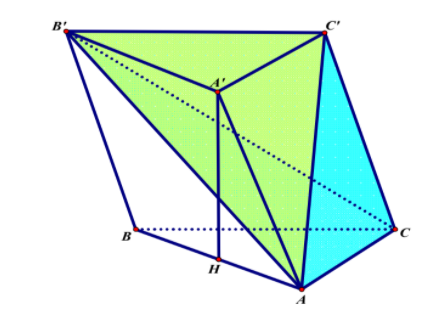
Ta có: $\large \left\{\begin{align}& V_{ACC'B'}=V_{AA'C'B'}=V_{ABC'B'}\\& V_{ABC.A'B'C'}=V_{ACC'B'}+V_{AA'C'B'}+V_{ABC'B'}\\\end{align}\right. $ $\large \Rightarrow V_{ACC'B'}=\dfrac{1}{3}V_{ABC.A'B'C'}$

Gọi H là trung điểm của $\large AB\Rightarrow A'H\perp (ABC)$

$\large \Rightarrow \widehat{(CC'; (ABC))}=\widehat{(AA'; (ABC))}=\widehat{A'AH}=60^\circ\Rightarrow A'H=AH.\tan 60^\circ=\dfrac{a\sqrt{3}}{2}$ 

$\large \Rightarrow V_{ACC'B'}=\dfrac{1}{3}.V_{ABC.A'B'C'}=\dfrac{1}{3}.\dfrac{1}{2}a.a.\dfrac{\sqrt{3}}{2}.\dfrac{a\sqrt{3}}{2}=\dfrac{a^3}{8}$