Cho hỗn hợp X gồm $\large CuO$ và $\large NaOH$ có tỉ lệ số mol 1:1 tá

Cho hỗn hợp X gồm $\large CuO$ và $\large NaOH$ có tỉ lệ số mol 1:1 tác dụng vừa đủ với dung dịch hỗn hợp $\large HCl $ 1M và $\large H_{2}SO_{4}$ 0,5M thu được dung dịch Y chỉ chứa m gam hỗn hợp muối trung hòa. Điện phân dung dịch Y với điện cực trơ, màng ngăn xốp cường độ I = 2,68A đến khi khối lượng dung dịch giảm 20,225 gam mất t giây thì dừng lại, thu được dung dịch Z. Cho m gam $\large Fe$ vào dung dịch Z sau khi phản ứng kết thúc thu được 0,9675m gam hỗn hợp 2 kim loại. Hiệu suất điện phân 100%. Giá trị của t gần nhất với:

• A.

  A. 11542

• B.

  B. 12654

• C.

  C. 12135

• D.

  D. 11946

- X (x mol $\large\ CuO$, x mol $\large\ NaOH$) + V lít ($\large\ HCl$ 1M và $\large\ H_2SO_4$ 0,5M) $\large\ \to$ dung dịch Y chỉ chứa muối trung hòa.

$\large\ \to$ Phản ứng xảy ra vừa đủ

Áp dụng bảo toàn điện tích $\large\ \to$ V + 0,5V.2 = 2x + x $\large\ \to$ V = 1,5x

$\large\ \to$ m = 64x + 23x + 35,5.1,5x + 96.0,5.1,5x = 212,25x

- Điện phân dung dịch Y $\large\ \to$ dung dịch Z (Phản ứng với $\large\ Fe \to$ 2 kim loại)

$\large\ \to$ Chứng tỏ phản ứng điện phân còn dư $\large\ Cu^{2+}$

Khối lượng 2 kim loại thu được < Khối lượng $\large\ Fe$ cho vào $\large\ \to$ Chứng tỏ trong dung dịch chứa $\large\ H^+$, ở anot $\large\ H_2O$ đã bị điện phân

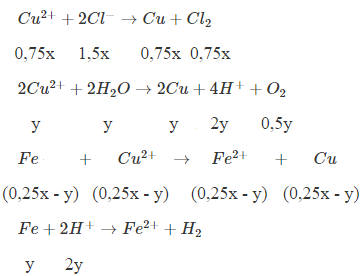
$\large\ \to$ m - 0,9675m = 56.(y + 0,25x - y) - 64.(0,25x - y)

$\large\ \to$ 64y - 2x = 0,0325m = 0,0325.212,25x $\large\ \to$ y = 0,139x

Có $\large\ m_{dd \ giảm} = m_{Cu} + m_{Cl_2} + m_{O_2}$

$\large\ m_{dd \ giảm} = 64.(0,75x + y) + 71.0,75x + 32.0,5y = 20,225g$

$\large\ \to \left\{\begin{matrix} x = 0,18 \\ y = 0,025
 & 
\end{matrix}\right.$

$\large\ t = \dfrac{(0,75.0,18 + 0,025).2.96500}{2,68} = 11523s$