Cho hình nón có thiết diện qua trục là tam giác vuông cân có cạnh huyề

Cho hình nón có thiết diện qua trục là tam giác vuông cân có cạnh huyền bằng $\large 2a \sqrt {2}$. Diện tích xung quanh của hình nón đã cho bằng

• A.

  $\large \sqrt {2} \pi a^{2}$

• B.

  $\large 2 \sqrt {2} \pi a^{2}$

• C.

  $\large 4 \pi a^{2}$

• D.

  $\large 4 \sqrt {2} \pi a^{2}$

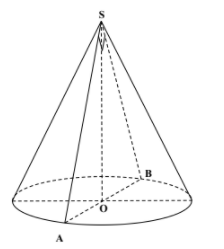
Thiết diện qua trục là tam giác $\large \Delta SAB$ vuông cân tại S, có $\large AB = 2a \sqrt {2}$ nên bán kính đáy $\large r = \dfrac {AB}{2} = a \sqrt {2}$
Đường sinh $\large l = SA = \sqrt {\dfrac {AB^{2}}{2}} = \sqrt {\dfrac {(2a \sqrt {2})^{2}}{2}} = 2a$
Vậy diện tích xung quanh của hình nón là $\large S_{xq} = \pi r l = \pi a \sqrt {2}.2a = 2 \sqrt {2} \pi a^{2}$