Cho hình lập phương $\Large ABCD.{A}'{B}'{C}'{D}'$. Côsin góc giữa hai

Cho hình lập phương $\Large ABCD.{A}'{B}'{C}'{D}'$.

Côsin góc giữa hai mặt phẳng $\Large ({A}'BC)$ và $\Large (AB{C}')$ bằng

• A.

  $\Large \dfrac{\sqrt{3}}{2}$.

• B.

  $\Large \dfrac{\sqrt{2}}{2}$.

• C.

  0.

• D.

  $\Large \dfrac{1}{2}$.

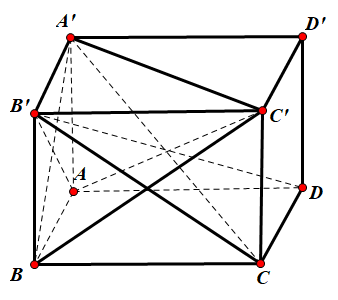
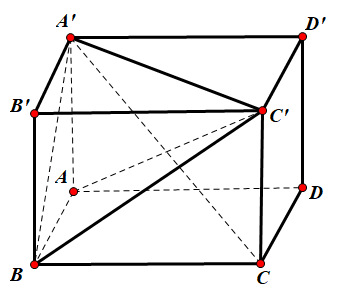
Cách 1:

Gọi $\Large \left(({A}'BC), (AB{C}')\right)=\alpha$.

Ta có $\Large \left\{\begin{align} & AB'\perp A'B \\ & AB'\perp BC \end{align}\right.$ $\Large \Rightarrow AB'\perp (A'BC)$.

Ta có $\Large \left\{\begin{align} & B'C\perp BC' \\ & B'C\perp AB \end{align}\right.$ $\Large \Rightarrow B'C\perp (ABC')$.

Suy ra $\Large \left((A'BC), (ABC')\right)=\widehat{(AB', B'C)}=\widehat{AB'C}=60^{\circ}$ (vì $\Large \Delta AB'C$ đều).

Vậy $\Large \cos \alpha=\cos 60^{\circ}=\dfrac{1}{2}$.

Cách 2:

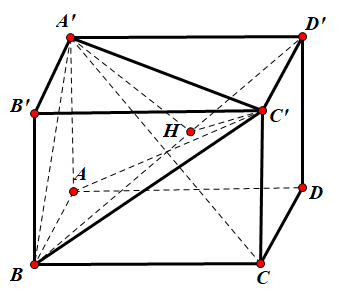
Gọi cạnh của hình lập phương là $\Large a$, ta có $\Large (A'BC)\cap (ABC')=BD'$.

Trong mặt phẳng $\Large (A'BC)$ từ $\Large A'$ kẻ $\Large A'H\perp BD'$. Do $\Large \Delta A'BD'$=$\Large \Delta C'BD'$ có $\Large BD'$ chung nên $\Large C'H\perp BD'$. Khi đó góc giữa hai mặt phẳng $\Large (A'BC)$ và $\Large (ABC')$ là góc giữa hai đường thẳng $\Large A'H$ và $\Large C'H$.

Xét $\Large \Delta A'HC'$ có $\Large A'H=C'H=\dfrac{a\sqrt{6}}{3}$, $\Large A'C'=a\sqrt{2}$.

Khi đó $\Large \cos \widehat{A'HC'}=\dfrac{A'H^2+C'H^2-A'C'^2}{2A'H.C'H}$=$\Large \dfrac{\left(\dfrac{a\sqrt{6}}{3}\right)^2+\left(\dfrac{a\sqrt{6}}{3}\right)^2-(a\sqrt{2})^2}{2.\dfrac{a\sqrt{6}}{3}.\dfrac{a\sqrt{6}}{3}}=-\dfrac{1}{2}$.

Do đó côsin góc giữa hai đường thẳng $\Large A'H$ và $\Large C'H$ bằng $\Large \dfrac{1}{2}$.

Vậy côsin góc giữa hai mặt phẳng $\Large (A'BC)$ và $\Large (ABC')$ bằng $\Large \dfrac{1}{2}$.