Cho hình lập phương ABCD.A'B'C'D'. Gọi $\Large \varphi$ là góc giữa ha

Cho hình lập phương ABCD.A'B'C'D'. Gọi $\Large \varphi$ là góc giữa hai mặt phẳng (A'BD) và (ABC). Tính $\Large tan\varphi.$

• A.

  $\Large tan\varphi=\dfrac{1}{\sqrt{2}}.$

• B.

  $\Large tan\varphi=\sqrt{\dfrac{2}{3}}.$

• C.

  $\Large tan\varphi=\sqrt{\dfrac{3}{2}}.$

• D.

  $\Large tan\varphi=\sqrt{2}.$

Chọn D

Gọi O là tâm hình vuông ABCD, ta có AO là hình chiếu vuông góc của A'O lên mặt phẳng (ABCD). Khi đó ta có $\Large \left\{\begin{align} & AO \perp BD \\ & {A}'O\perp BD \end{align}\right.$ suy ra $\Large \varphi=\widehat{{A}'OA}.$

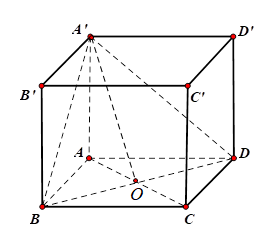
Ta có $\Large AO=\dfrac{AC}{2}=\dfrac{AB\sqrt{2}}{2}=\dfrac{A{A}'\sqrt{2}}{2};tan\varphi=tan\widehat{{A}'OA}=\dfrac{A{A}'}{AO}=\sqrt{2}.$