Cho hình lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm của A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chứa điểm B gọi là V1. Gọi V là thể tích khối lăng trụ. Tính tỉ số V1V
Đáp án án đúng là: A
Lời giải chi tiết:
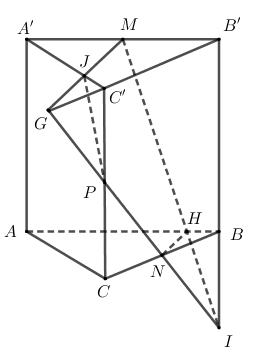
Gọi I=NP∩BB′,G=NP∩B′C′,J=MG∩A′C′,H=IM∩AB
Ta có IHIM=INIG=IBIB′=13,GC′GB′=GPGI=13,GJGM=12
Ta có VI.B′MG=13d(I,(B′MG)).SB′MG=13⋅32d(B,(B′MG)).12d(G,B′M).B′M
=14d(B,(B′MG)).d(G,B′M).12B′A′=38.13.d(B,(B′MG)).d(G,B′M).B′A′=38V
VI.BHNVI.B′MG=IBIB′.IHIM.INGI=127⇒VI.BHN=127VI.B′MG=172V
VG.C′JPVG.B′MI=GC′GB′.GJGM.GPGI=118⇒VG.C′JP=118VI.B′MG=148V
Khi đó V1=VI.B′MG−VI.BHN−VG.C′JP=38V−148V−172V=49144V⇒V1V=49144
Đáp án A
Xem thêm các bài tiếp theo bên dưới