Cho hình lăng trụ tam giác đều $\large ABC.A'B'C'$ có AB = a , đường t

Cho hình lăng trụ tam giác đều $\large ABC.A'B'C'$ có AB = a , đường thẳng A'B tạo với mặt phẳng $\large (BCC'B')$ một góc $\large 30^\circ$. Tính thể tích khối lăng trụ $\large ABC. A' B' C'$

• A.

  $\large \dfrac{a^3\sqrt{6}}{4}$

• B.

  $\large \dfrac{a^3\sqrt{3}}{4}$

• C.

  $\large \dfrac{3a^3}{4}$

• D.

  $\large \dfrac{3a^3}{2}$

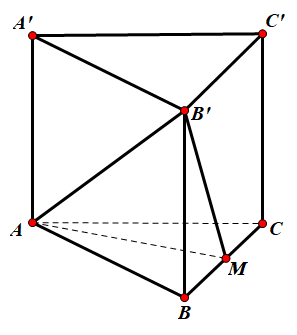
Gọi M là trung điểm BC. Suy ra, $\large AM\perp BC$

Vì $\large ABC.A'B'C'$ là lăng trụ tam giác đều nên $\large AM\perp (BCC'B')$

Vì $\large MB'$ là hình chiếu của đường thẳng $\large AB'$ lên mặt phẳng $\large (BCC'B')$ nên góc giữa đường thẳng $\large AB'$ tạo với mặt phẳng $\large (BCC'B')$ là góc $\large \widehat{AB'M}$. Ta được $\large \widehat{AB'M}=30^\circ$

 .Xét tam giác AB M' vuông tại M, ta có: $\large AB'=\dfrac{AM}{\sin 30^\circ}=a\sqrt{3}$

Xét tam giác AB B' vuông tại B , ta có: $\large BB'=\sqrt{AB'^2-AB^2}=a\sqrt{2}$

Vậy $\large V_{ABC.A'B'C'}=S_{\Delta ABC}.BB'=\dfrac{a^2\sqrt{3}}{4}.a\sqrt{2}=\dfrac{a^2\sqrt{6}}{4}$