Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a .

Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a . Tính cosin của góc giữa hai đường thẳng AB ' và BC '

• A. $\Large -\dfrac{1}{4}$
• B. $\Large \dfrac{3}{4}$
• C. $\Large \dfrac{1}{4}$
• D. $\Large \dfrac{1}{3}$

Chọn C

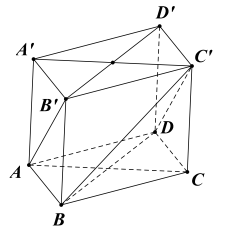
Ta dựng hình lăng trụ đúng ABCD.A'B'C'D'

Ta có $\Large D C^{\prime} \| A B^{\prime} \Rightarrow\left(\widehat{\left.A B^{\prime}, B C^{\prime}\right)}=\left(\widehat{\left.B C^{\prime}, DC ^{\prime}\right)}\right.\right.$

Xét tam giác BC'D. Ta có $\Large B C^{\prime}=D C^{\prime}=a \sqrt{2} ; B D=a \sqrt{3}$

$\Large \Rightarrow \cos \widehat{B C^{\prime} D}=\dfrac{B C^{\prime 2}+D C^{\prime 2}-B D^{2}}{2 \cdot B C^{\prime} \cdot D C^{\prime}}=\dfrac{1}{4}$. Vậy cosin của góc giữa hai đường thẳng AB' và BC' bằng $\Large \dfrac{1}{4}$