Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, $\

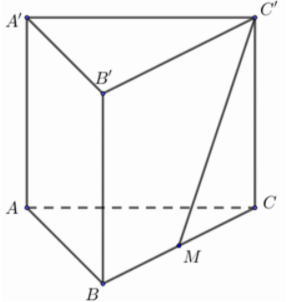
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, $\Large \widehat{BAC}=120^{o}, AD=2a,AA'=a\sqrt{2}$. Gọi M là trung điểm của cạnh BC (tham khảo hình vẽ)

Khoảng cách giữa hai đường thẳng C'M và AB bằng

• A. $\Large \dfrac{2a\sqrt{66}}{11}$
• B. $\Large \dfrac{a\sqrt{66}}{22}$
• C. $\Large \dfrac{a\sqrt{22}}{11}$
• D. $\Large \dfrac{a\sqrt{66}}{11}$

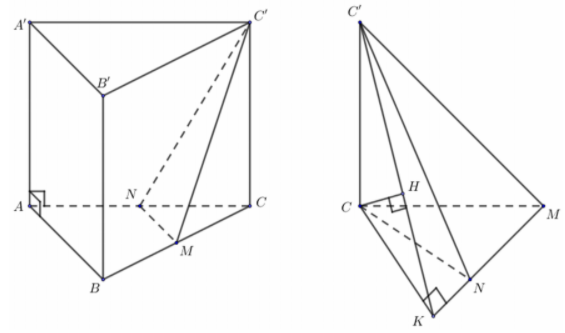Gọi N là trung điểm của AC, ta có MN//AB (vì M là trung điểm của BC)

$\Large \Rightarrow AB\\(C'MN)\Rightarrow d(AB,C'M)=d(AB,(C'MN))=d(B,(C'MN))=d(C,(C'MN))$

Trong tam giác CMN, kẻ $\Large CK\perp MN$

Ta có $\Large \widehat{CNM}=\widehat{CAB}=120^{o}\Rightarrow \widehat{CNK}=60^{o};NC=\dfrac{1}{2}AC=a$

Xét $\Large \Delta CKN$ vuông tại K, ta có $\Large CK=CN.\sin\widehat{CNK}=\dfrac{a\sqrt{3}}{2}$

Trong $\Large \Delta CKC'$, kẻ $\Large CH\perp C'K$. Ta có $\Large \left\{\begin{align}&MK\perp CK\\&MK\perp CC'\\\end{align}\right.$ $\Large \Rightarrow MK\perp (CC'K)\Rightarrow MK\perp CH$

$\Large \Rightarrow CH\perp (C'MN)\Rightarrow d(C,(C'MN))=CH$

Trong tam giác $\Large C'CK$ vuông tại C, ta có $\Large CH=\dfrac{CK.CC'}{\sqrt{CK^{2}+CC'^{2}}}=\dfrac{\dfrac{a\sqrt{3}}{2}.a\sqrt{2}}{\sqrt{\left(\dfrac{a\sqrt{3}}{2}\right)^{2}+(a\sqrt{2})^{2}}}=\dfrac{a\sqrt{66}}{11}$

Vậy $\Large d(AB,C'M)=\dfrac{a\sqrt{66}}{11}$