Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh có độ dài bằng 2 (

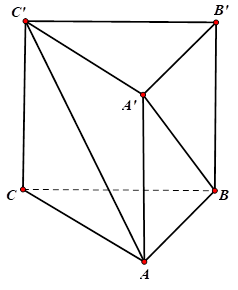
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh có độ dài bằng 2 (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng AC' và A'B.

• A. $\Large \dfrac{2}{\sqrt{5}}.$
• B. $\Large \dfrac{\sqrt{3}}{2}.$
• C. $\Large \dfrac{1}{\sqrt{2}}.$
• D. $\Large \dfrac{\sqrt{3}}{\sqrt{5}}.$

Chọn A

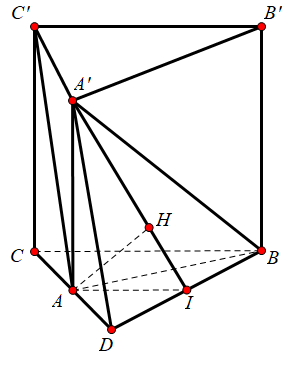
Gọi D là điểm đối xứng của C qua A ta có tứ giác ADA'C' là hình bình hành do đó $\Large {A}'D // A{C}',$ suy ra khoảng cách $\Large d(A{C}', B{A}')=d\big(A{C}', ({A}'BD)\big)=d\big(A,({A}'BD)\big).$

Theo giả thiết ABC.A'B'C' là lăng trụ đều nên $\Large A{A}'\perp (ABC)$ hay $\Large A{A}'\perp (BCD)$ suy ra $\Large A{A}'\perp BD \ (1).$

Ta có $\Large \Delta ABD$ có $\Large AB=AD$ nên là tam giác cân tại A, gọi I là trung điểm BD ta có $\Large AI\perp BD \ (2).$

Xét tam giác $\Large \Delta BCD$ có A, I lần lượt là trung điểm của DC, DB nên $\Large AI=\dfrac{1}{2}BC=1.$

Trong mặt phẳng (A'AI) dựng $\Large AH\perp {A}'I; H \in {A}'I \ (3).$

Từ (1) và (2) suy ra $\Large BD\perp ({A}'AI) \Rightarrow BD \perp AH \ (4).$

Từ (3) và (4) suy ra $\Large AH \perp ({A}'BD)$ do đó khoảng cách $\Large d\big(A,(SBD)\big)=AH.$

Trong tam giác A'AI vuông tại A có $\Large AH=\dfrac{AI.A{A}'}{\sqrt{AI^2+(A{A}')^2}}=\dfrac{2}{\sqrt{5}}.$