Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$ có $\large AB=x,AD=3$ góc

MỤC LỤC
Câu hỏi:
Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$ có $\large AB=x,AD=3$ góc giữa đường thẳng $\large A'C$ và mặt phẳng $\large (ABB'A')$ bằng $\large 30^{\circ}$.Tìm $\large x$ để khối hộp chữ nhật có thể tích lớn nhất.
Đáp án án đúng là: B
Lời giải chi tiết:
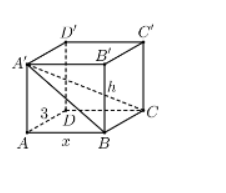
Xác định $\large 30^{\circ}=\widehat{{A^{\prime} C,\left(ABB^{\prime} A^{\prime}\right)}}=\widehat{{C A^{\prime} B}}$
Đặt $\large BB^{\prime}=h(h>0)$
Ta có:
$\large \tan \widehat{{C A^{\prime} B}}=\frac{B C}{A^{\prime} B} \Leftrightarrow \tan 30^{\circ}=\frac{3}{\sqrt{x^{2}+h^{2}}} \Leftrightarrow x^{2}+h^{2}=27$
Khi đó $\large V=S_{ABCD}.BB^{\prime}=3xh=3x\sqrt{27-x^{2}}\leq 3\left(\frac{x^{2}+27-x^{2}}{2}\right)=\frac{81}{2}$
Dấu "=" xảy ra $\large\Leftrightarrow x^{2}=27-x^{2}\Rightarrow x=\frac{3\sqrt{6}}{2}$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp $\large SA=x(0< x< \sqrt{3})$, tất cả cách cạnh còn lại
- Một người đã cắt tấm bìa cactong và đặt kích thước như hình vẽ. Sau đó
- Từ hình vuông có cạnh bằng 6 người ta cắt bỏ các tam giác vuông cân tạ
- Bên trong một căn nhà bỏ hoang hình lập phương thể tích $\Large 1000m^
- Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích $