Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy. Hỏi góc gi

Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy. Hỏi góc giữa hai mặt phẳng (SAB) và (SAD) gần nhất với kết quả ào dưới đây?

• A. $\Large 89^{0} 34^{\prime}$
• B. $\Large 61^{0} 28^{\prime}$
• C. $\Large 70^{0} 32^{\prime}$
• D. $\Large 109^{0} 29^{\prime}$

Chọn C

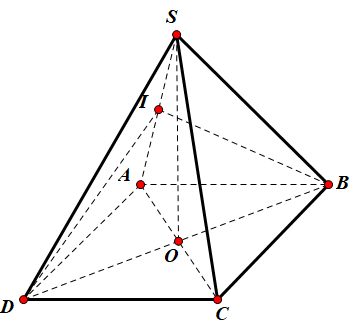
Gọi $\Large O=A C \cap B D$, chop S.ABCD là chóp đều nên $\Large S O \perp(A B C D)$

Suy ra $\Large S O \perp B D$ mà $\Large$\Large A C \perp B D$(do ABCD là hình vuông) nên$\Large B D \perp(S A C) \Rightarrow B D \perp S A$

Kẻ $\Large O I \perp S A \Rightarrow S A \perp(I B D) \Rightarrow S A \perp I B, S A \perp I D$

Do đó $\Large ((S A B),(S A D))=(\overline{I B, I D})$

Giả dử cạnh bên và cạnh đáy của chóp cùng bằng a.

Do IB, ID lần lượt là trung tuyến của hai tam giác đều SAB, SAD cạnh a nên $\Large I B=I D=\dfrac{a \sqrt{3}}{2}$.

Mặt khác, ta có $\Large B D=\sqrt{B C^{2}+C D^{2}}=a \sqrt{2}$

Xét tam giác IBD có $\Large B D^{2}=I B^{2}+I D^{2}-2 \cdot I B \cdot I D \cdot \cos \widehat{B I D}$

$\Large \Leftrightarrow 2 a^{2}=\dfrac{3}{4} a^{2}+\dfrac{3}{4} a^{2}-2 \cdot \dfrac{a \sqrt{3}}{2} \cdot \dfrac{a \sqrt{3}}{2} \cdot \cos \widehat{B I D}$ $\Large \Leftrightarrow \cos \widehat{B I D}=\dfrac{1}{3} \Rightarrow \widehat{B I D} \approx 70^{0} 31^{\prime}$