Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy và chiều cao đều

Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy và chiều cao đều bằng $\Large a$. Diện tích xung quanh của hình nón đỉnh $\Large S$ có đáy là hình tròn nội tiếp tứ giác $\Large ABCD$ bằng

• A.

  $\Large \dfrac{\pi a^2\sqrt{5}}{8}$.

• B.

  $\Large \dfrac{\pi a^2\sqrt{5}}{2}$.

• C.

  $\Large \dfrac{\pi a^2\sqrt{5}}{6}$.

• D.

  $\Large \dfrac{\pi a^2\sqrt{5}}{4}$.

Chọn D

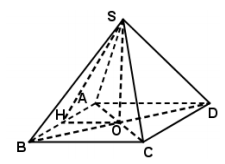
Gọi $\Large H$ là trung điểm $\Large AB$. Hình nón có hình tròn đáy tâm $\Large O$, bán kính $\Large r=OH=\dfrac{a}{2}$ và độ dài đường sinh $\Large l=SH=\sqrt{SO^2+OH^2}=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}$.

Vậy diện tích xung quanh của hình nón đã cho bằng $\Large S_{xq}=\pi rl=\pi .\dfrac{a}{2}.\dfrac{a\sqrt{5}}{2}=\dfrac{\pi a^2\sqrt{5}}{4}$.