Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, $\Large \angle B A D

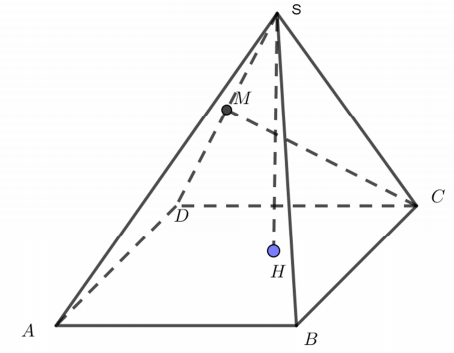
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, $\Large \angle B A D =60^{\circ},  SB=SD =SC$, M là trung điểm của SD, H là hình chiếu của S trên mặt phẳng (ABCD). Tính khoảng cách giữa hai đường SH và CM

• A. $\Large \dfrac{a \sqrt{17}}{14}$
• B. $\Large \dfrac{a \sqrt{3}}{14}$
• C. $\Large \dfrac{a \sqrt{7}}{7}$
• D. $\Large \dfrac{a \sqrt{3}}{7}$

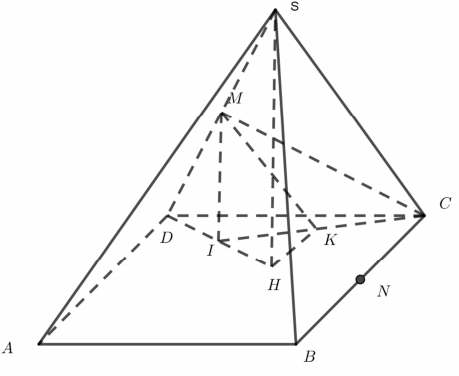
Ta có: ABCD là hình thoi có $\Large \angle B A D=60^{\circ}$ nên $\Large \Delta B C D$ là tam giác đều cạnh a

Có $\Large \left\{\begin{array}{l} S B=S C=S D \\ S H \perp(A B C D) \end{array} \Rightarrow\right.$ H là trọng tâm  $\Large \Delta B C D$

Gọi I, N lần lượt là trung điểm của DH, BC.

$\Large \Delta SDH$ có MI là đường trung bình

$\Large \Rightarrow M I / / S H \Rightarrow S H / /(M I C)$ $\Large \Rightarrow d(S H, C M)=d(S H,(M C I))=d(H,(C M I))=H K$

HK là đường cao của $\Large \Delta IHC$

Ta có: $\Large S_{\Delta IH C}=\dfrac{1}{2} \cdot I H \cdot C N=\dfrac{1}{2} \cdot \dfrac{1}{3} \cdot D N \cdot C N=\dfrac{1}{6} \cdot \dfrac{a \sqrt{3}}{2} \cdot \dfrac{a}{2}=\dfrac{a^{2} \sqrt{3}}{24}$

$\Large S_{\Delta IHC}=\dfrac{1}{2} \cdot H K \cdot C I \Rightarrow H K=\dfrac{2 S _{\Delta IHC}}{C I}$

$\Large \Delta DIC$ có: $\Large I C=\sqrt{D I^{2}+D C^{2}-2 . D I \cdot D C \cdot \cos 30^{\circ}}=\dfrac{\sqrt{7}}{\sqrt{12}} a$

Vậy $\Large H K=\dfrac{2 S _{\Delta IHC}}{I C}=\dfrac{2 a ^{2} \sqrt{3}}{24} \cdot \sqrt{\dfrac{7}{12}} \cdot a=\dfrac{a \sqrt{7}}{14}$