Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=2a

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=2a và vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của SD. Tính khoảng cách d giữa hai đường thẳng SB và CM
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Cách 1: Sử dụng phương pháp dựng khoảng cách:
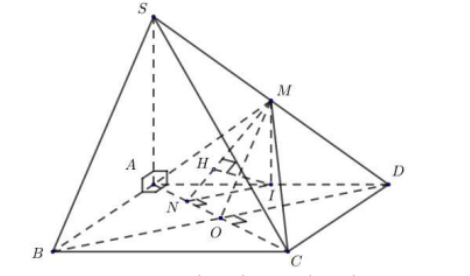
Gọi O=AC∩BD⇒SB//OM, mà OM⊂(AMC)⇒SB//(AMC)
ta có: d(SB,CM)=d(SB,(AMC))=d(B,(AMC))=d(D,(AMC))(1)
Gọi I là trung điểm của AD⇒MI//SA mà SA⊥(ABCD)⇒MI⊥(ABCD)
Lại có: CI∩(AMC)=A⇒d(D,(AMC))2d(I,(AMC))(2)
Từ (1) và (2), suy ra: d(SB,CM)=2d(I,(AMC))(3)
Gọi N là trung điểm của AO ⇒IN//OD mà OD⊥AC⇒IN⊥AC
Ta có: {AC⊥INAC⊥MI ⇒AC⊥(MIN)⇒(MIN)⊥(MAC), mà (MIN)∩(MAC)=MN
Trong (MIN), kẻ IH⊥MN⇒IH⊥(MAC)⇒d(I,(MAC))=IH (4)
Xét tam giác MIN vuông tại I, MI=12SA=a,IN=12OD=14BD=a√24
⇒IH=IN.IM√IN2+IM2=a.a√24√a2+(a√24)2⇒IH=a3 (5)
Từ (3), (4) và (5) suy ra: d(SB,CM)=2a3
Cách 2: Sử dụng phương pháp tọa độ hóa
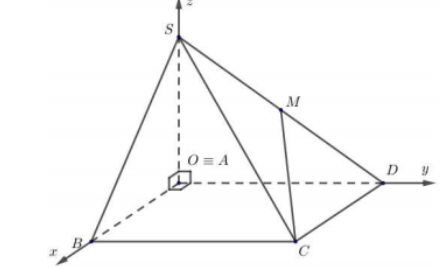
Chọn hệ trục tọa độ như hình vẽ, ta có:
B(a,0,0),S(0,0,2a),C(a,a,0),M(0;a2,a)
⇒→SB=(a;0;−2a),→MC=(a;a2;−a),→BC=(0;a;0)
⇒[→SB,→MC]=(a2;−a2;a2a)⇒[→SB,→MC].→BC=−a3
Vậy d(SB,CM)=[→SB,→MC].→BC[→SB,→MC]=a3√a4+a4+a44=2a3
Xem thêm các bài tiếp theo bên dưới