Cho hình chóp S.ABC có tam giác ABC vuông tại A, $\large AB=2a, AC=3a$

Cho hình chóp S.ABC  có tam giác ABC vuông tại A, $\large AB=2a, AC=3a$, SA vuông góc với (ABC), SA =5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC

• A. $\large R=\dfrac{a\sqrt{38}}{4}$
• B. $\large R=a\sqrt{38}$
• C. $\large R=\sqrt{38}$
• D. $\large R=\dfrac{a\sqrt{38}}{2}$

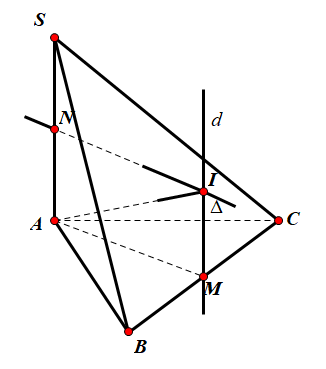
Gọi M, N lần lượt là trung điểm của BC và SA.
Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC .
Dựng đường thẳng d qua M và d vuông góc với (ABC)

Ta có: $\large \left\{\begin{align}& d\perp (ABC)\\& SA\perp (ABC)\\\end{align}\right.$ $\large \Rightarrow d// SA$

Trong mặt phẳng (SA, d), kẻ đường trung trực $\large \Delta$ của SA, $\large \Delta $ qua N và cắt d tại I.

Do $\large I\in d\Rightarrow IA=IB=IC (1)$

Mà $\large I\in \Delta \Rightarrow IS=IA (2)$

Từ (1) và (2) suy ra $\large IA=IB=IC=IS$

Suy ra I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC và $\large IA=IB=IC=IS=R$
Trong tam giác ABC vuông tại A, ta có:

$\large BC=\sqrt{AB^2+AC^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\Rightarrow AM=\dfrac{BC}{2}=\dfrac{a\sqrt{13}}{2}$

Do tứ giác ANIM là hình chữ nhật, suy ra $\large NI=AM=\dfrac{a\sqrt{13}}{2}$

Xét tam giác AIN vuông tại N . Có $\large IA=\sqrt{NI^2+AN^2}=\sqrt{\dfrac{13a^2}{4}+\dfrac{25a^2}{4}}=\dfrac{a\sqrt{38}}{2}$

Vậy: $\large R=\dfrac{a\sqrt{38}}{2}$

Công thức tính nhanh:
Tổng quát: Cho hình chóp S.ABC có $\large SA\perp (ABC)$. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC được tính bởi công thức: $\large R=\sqrt{r^2+\dfrac{h^2}{4}}$

Trong đó: r là bán kính đường tròn ngoại tiếp đáy, h là chiều cao của hình chóp.

Theo giả thiết ta có: $\large r=\dfrac{BC}{2}=\dfrac{a\sqrt{13}}{2}, h=SA=5a$

Vậy $\large R=\sqrt{\dfrac{13a^2}{4}+\dfrac{25a^2}{4}}=\dfrac{a\sqrt{38}}{2}$