Cho hàm số y = f(x) liên tục trên $\Large \mathbb{R}$ có đồ thị như hì

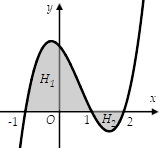
Cho hàm số y = f(x) liên tục trên $\Large \mathbb{R}$ có đồ thị như hình vẽ. Biết $\large H_1$ có diện tích bằng 7 (đvdt) , $\large H_2$ có diện tích bằng 3 (đvdt).

Tính $\large I=\int_{-2}^{-1} (2x+6)f(x^2+6x+7) dx$

• A. 11 (đvdt)
• B. 4 (đvdt)
• C. 1 (đvdt)
• D. 10 (đvdt)

Dựa vào đồ thị ta thấy: $\large \left\{\begin{align}& S_{H_1}=\int_{-1}^1 f(x)dx\\& S_{H_2}=\int_1^2 [-f(x)] dx\\\end{align}\right.$  $\large \Rightarrow \left\{\begin{align}& \int_{-1}^1 f(x)dx=7\\& \int_1^2 f(x)dx=-3\\\end{align}\right.$ 

Xét: $\large I=\int_{-2}^{-1} (2x+6) f(x^2+6x+7) dx$ 

Đặt: $\large t=x^2+6x+7\Rightarrow dt=(2x+6)dx$ . Đổi cận $\large \left\{\begin{align}& x=-2\Rightarrow t=-1\\& x=-1\Rightarrow t=2\\\end{align}\right.$ 

Khi đó: $\large I=\int_{-1}^2 f(t)dt=\int_{-1}^2 f(x)dx=\int_{-1}^1 f(x)dx+\int_1^2 f(x)dx=7+(-3)=4 (dvdt)$ 

Vậy $\large I=4 (dvdt)$