Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\Large AB=3a,
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a,BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi SC và đáy bằng 60∘. Gọi M là trung điểm của AC, tính khoảng cách giữa hai đường thẳng AB và SM.
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
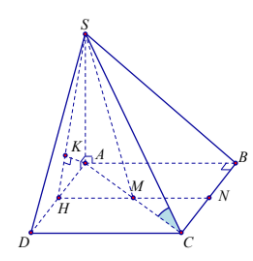
Ta có: (SC,(ABC))=^SCA=600⇒AC=5a,SA=5a√3.
Gọi N là trung điểm BC ⇒AB//(SMN)⇒d(AB,SM)=d(A,(SMN)).
Dựng AH⊥MN tại H trong (ABC).
Dựng AK⊥SH tại K trong (SAH).
⇒AK⊥(SMN) tại K nên d(A,(SMN))=AK⇒d[AB,SM]=AK.
AH=NB=2a.
1AK2=1AH2+1SA2=14a2+175a2=79300a2⇒AK=10a√3√79.
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số f(x)=13x3+2x2+(m+1)x+5. Tìm tất cả các
- Trên một chiếc đài Radio FM có vạch chia để người dùng có thể dò sóng
- Cho đồ thị hai hàm số f(x)=2x+1x+1 và $\Large g(x)=
- Một hình trụ có bán kính đáy bằng 5 và khoảng cách giữa hai đáy bằng 7
- Xét hàm số f(x) liên tục trên đoạn [0; 1] và thỏa mãn $\Large