Cho hình chóp S. ABCD có đáy là hình vuông cạnh a, cạnh bên $\large SD

Cho hình chóp S. ABCD có đáy là hình vuông cạnh a, cạnh bên $\large SD=\dfrac{a\sqrt{17}}{2}$. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của đoạn thẳng AB. Gọi E là trung điểm của AD. Tính khoảng cách giữa hai đường thẳng HE và SB

• A. A. $\large \dfrac{a\sqrt{3}}{2}$
• B. B. $\large \dfrac{a}{2}$
• C. C. $\large \dfrac{a\sqrt{21}}{7}$
• D. D. $\large \dfrac{a\sqrt{3}}{5}$

Chọn D

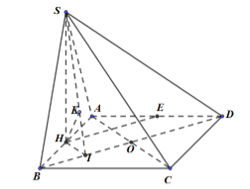
Ta có: $\large HE// (SBD)\Rightarrow  d(HE, SB)= d(HE, (SBD))= d(H, (SBD))$
Gọi O là tâm của hình vuông, I là trung điểm của BO
$\large \Rightarrow  HI//AC mà $\large BD\perp AC\Rightarrow  HI\perp BD$
Mà $\large SH\perp BD\Rightarrow  BD\perp (SHI)\Rightarrow  BD\perp HK\, (K\in SI,\, HK\perp SI)$
$\large \Rightarrow  d(H, (SBD))= HK$
$\large HD=\sqrt{a^2+\dfrac{a^2}{4}}=\dfrac{a\sqrt{5}}{2},\, SH=\sqrt{SD^2- HD^2}= \sqrt{\dfrac{17a^2}{4}- \dfrac{5a^2}{4}}= a\sqrt{3}$
$\large HI= \dfrac{1}{2}AO= \dfrac{1}{2}.\df{a\sqrt{2}}{2}= \dfrac{a\sqrt{2}}{4}$
$\large \dfrac{1}{HK^2}= \dfrac{1}{SH^2}+\dfrac{1}{HI^2}\Leftrightarrow \dfrac{1}{HK^2}= \dfrac{1}{3a^2}+ \dfrac{8}{a^2}= \dfrac{25}{3a^2}\Rightarrow  HK=\dfrac{a\sqrt{3}}{5}$
Vậy $\large d(HE, SB)= \dfrac{a\sqrt{3}}{5}$