Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA v

Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi E, F lần lượt là trung điểm của cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là 

• A. $\large \widehat{CSF}$
• B. $\large \widehat{BSF}$
• C. $\large \widehat{BSE}$
• D. $\large \widehat{CSE}$

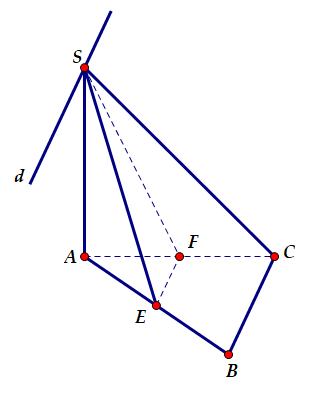
Gọi (d) là đường thẳng đi qua S và song song với EF
Vì EF là đường trung bình tam giác ABC suy ra $\large EF// BC$
Khi đó: $\large d//EF//BC\Rightarrow  (SEF)\cap (SBC)= (d)$ (1)
Ta có: $\large \left\{\begin{align}& SA\perp BC\, (SA\perp (ABC))\\& AB\perp BC\\\end{align}\right.$ $\large \Rightarrow  BC\perp (SAB)\Rightarrow  $ $\large \left\{\begin{align}& BC\perp SE\\& BC\perp SB\\\end{align}\right.$ (2)
Từ (1) và (2) suy ra: $\large \left\{\begin{align}& (d)\perp SE\\& (d)\perp SB\\\end{align}\right.$ $\large \Rightarrow ((SEF), (SBC))= (SE, SB) = \widehat BSE$