Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a và $\large SA=

Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a và $\large SA= SB= SC= b$. Gọi G là trọng tâm $\large \Delta ABC$. Độ dài SG là

• A. $\large \dfrac{\sqrt{9b^2+3a^2}}{3}$
• B. $\large \dfrac{\sqrt{b^2-3a^2}}{3}$
• C. $\large \dfrac{\sqrt{9b^2-3a^2}}{3}$
• D. $\large \dfrac{\sqrt{b^2+3a^2}}{3}$

Chọn C

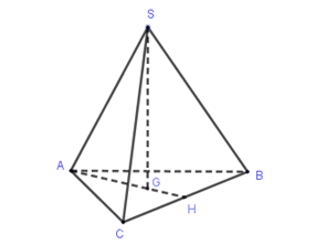
Theo bài ra hình chóp S. ABC là hình chóp tam giác đều
Gọi H là trung điểm của BC, ta có: $\large SG\perp (ABC),\, G\in AH$
Mà $\large AH= \dfrac{a\sqrt{3}}{2}\Rightarrow  AG= \dfrac{2}{3}AH= \dfrac{a\sqrt{3}}{3}$
Tam giác SAG vuông tại G nên theo định lý Pi – ta – go ta có:
$\large SG= \sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{a^2}{3}}=\sqrt{\dfrac{3b^2-a^2}{3}}=\dfrac{\sqrt{9b^2-3a^2}}{3}$