Cho hình chóp $\large S.ABCD$ có SA vuông góc với mặt phẳng $\large (A
MỤC LỤC
Câu hỏi:
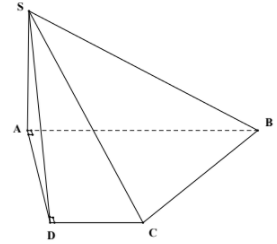
Cho hình chóp $\large S.ABCD$ có SA vuông góc với mặt phẳng $\large (ABCD), SA = a \dfrac {\sqrt {2}}{2}$, đáy ABCD là 2 hình thang vuông tại A và D có $\large AB = 2 AD = 2DC = a$ (Hình vẽ minh họa). Góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABCD)$ bằng

Cho hình chóp $\large S.ABCD$ có SA vuông góc với mặt phẳng $\large (ABCD), SA = a \dfrac {\sqrt {2}}{2}$, đáy ABCD là 2 hình thang vuông tại A và D có $\large AB = 2 AD = 2DC = a$ (Hình vẽ minh họa). Góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABCD)$ bằng

Đáp án án đúng là: D
Lời giải chi tiết:
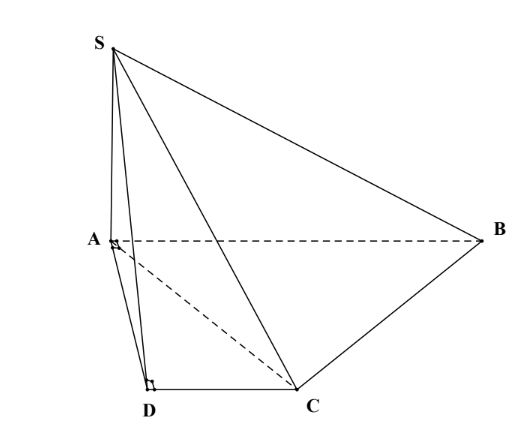
Ta có: $\large (SBC) \cap (ABCD) = BC$.
Vì ABCD là hình thang vuông tại A và D có $\large AB = 2 AD = 2DC = a \Rightarrow AC \perp BC$ (1)
$\large SA \perp ( ABCD) \Rightarrow SA \perp BC$ (2)
Từ (1) và (2) suy ra: $\large BC \perp SC$ nên góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABCD)$ bằng góc $\large \widehat{SCA}$
Trong tam giác vuông DAC có $\large AD = DC = \dfrac {a}{2} \Rightarrow AC = \dfrac {a \sqrt {2}}{2}$
Trong tam giác vuông ASC có $\large SA = AC = \dfrac {a \sqrt {2}}{2} \Rightarrow \widehat{SCA} = 45^{\circ}$
Góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABCD)$ bằng $\large \widehat{SCA} = 45^{\circ}$
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số $\large y = f (x)$ liên tục trên $\large \mathbb{R}$ có $\l
- Giá trị nhỏ nhất của hàm số $\large f(x) = x^{3} + 3x^{2} - 9x - 7 = 0
- Với $\large a, b$ là các số thực dương tùy ý và $\large a \neq 1$, đặt
- Cho hàm số $\large y = x^{4} - 3x^{2} - 3$, có đồ thị hình vẽ dưới đây
- Tập nghiệm của bất phương trình $\large log_{2}^{2} (2x) - 5 log_{2} x