Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình chữ nhật, $

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình chữ nhật, $\Large AB=a, AD=2a.$ Tam giác $\Large SAB$ cân tại $\Large S$ và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng $\Large SC$ và mặt phẳng $\Large (ABCD)$ bằng $\Large 45^{\circ}.$ Gọi $\Large M$ là trung điểm $\Large SD,$ hãy tính theo $\Large a$ khoảng cách từ $\Large M$ đến mặt phẳng $\Large (SAC).$

• A.

  A. $\Large d=\dfrac{2a\sqrt{1513}}{89}.$

• B.

  B. $\Large d=\dfrac{a\sqrt{1315}}{89}.$

• C.

  C. $\Large d=\dfrac{2a\sqrt{1315}}{89}.$

• D.

  D. $\Large d=\dfrac{a\sqrt{1513}}{89}.$

Chọn D

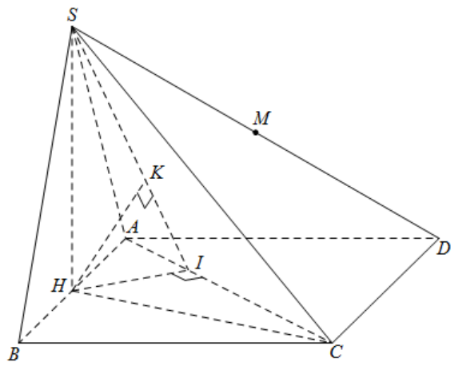
Gọi $\Large H$ là trung điểm của $\Large AB$

$\Large \Rightarrow SH \perp AB$ ($\Large \Delta SAB$ cân tại $\Large S$).

Ta có $\Large \left\{\begin{align} &(SAB) \cap (ABCD) =AB \\ & (SAB)\perp (ABCD) \\ & SH \perp AB (cmt) \end{align}\right.$ $\Large \Rightarrow SH\perp (ABCD).$

Vì $\Large SH\perp (ABCD),$ nên hình chiếu vuông góc của đường thẳng $\Large SC$ lên mặt phẳng $\Large (ABCD)$ là $\Large HC$

$\Large \Rightarrow\widehat{\big(SC, (ABCD)\big)}=\widehat{(SC, HC)}$ $\Large =\widehat{SCH}=45^{\circ}.$

$\Large \Delta HBC$ vuông tại $\Large B$, có

$\Large HC=\sqrt{HB^2+BC^2}$ $\Large =\sqrt{\bigg(\dfrac{AB}{2}\bigg)^2+BC^2}$ $\Large =\sqrt{\bigg(\dfrac{a}{2}\bigg)^2+(2a)^2}$ $\Large =\dfrac{a\sqrt{17}}{2}.$

$\Large \Delta SHC$ vuông cân tại $\Large H$, suy ra $\Large SH=HC=\dfrac{a\sqrt{17}}{2}.$

Ta có: $\Large \dfrac{d\big(M, (SAC)\big)}{d\big(D,(SAC)\big)}=\dfrac{MS}{DS}=\dfrac{1}{2}$ $\Large \Rightarrow d\big(M, (SAC)\big)=\dfrac{1}{2}d\big(D, (SAC)\big)=\dfrac{1}{2}d\big(B, (SAC)\big).$

Mặt khác $\Large \dfrac{d\big(B, (SAC)\big)}{d\big(H,(SAC)\big)}=\dfrac{BA}{HA}=2$ $\Large \Rightarrow d\big(B, (SAC)\big)=2d\big(H, (SAC)\big).$

Từ đó $\Large d\big(M,(SAC)\big)=d\big(H, (SAC)\big).$

Kẻ $\Large HI\perp AC$ tại $\Large I$ và kẻ $\Large HK\perp SI$ tại $\Large K.$

Ta có $\Large \left\{\begin{array}{l} AC\perp HI  (gt) \\ AC\perp SH \big(SH\perp (ABCD)\big) \end{array}\right.$ $\Large \Rightarrow AC\perp (SHI)$ $\Large \Rightarrow AC\perp HK.$

Ta có $\Large \left\{\begin{array}{l} HK \perp SI (gt) \\ HK\perp AC (cmt) \end{array}\right.$ $\Large \Rightarrow HK\perp (SAC)$ $\Large \Rightarrow d\big(H, (SAC)\big)=HK.$

$\Large \Delta ABC$ vuông tại $\Large B$, có $\Large AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+(2a)^2}=a\sqrt{5}.$

$\Large \Delta AIH \sim \Delta ABC$ $\Large \Rightarrow \dfrac{AI}{AB}=\dfrac{IH}{BC}=\dfrac{AH}{AC}$ $\Large \Rightarrow IH=\dfrac{BC.AH}{AC}=\dfrac{BC.AB}{2AC}=\dfrac{2a.a}{2.a\sqrt{5}}=\dfrac{a\sqrt{5}}{5}.$

$\Large \Delta SHI$ vuông tại $\Large H$, có $\Large HK=\dfrac{SH.HI}{\sqrt{SH^2+HI^2}}$ $\Large =\dfrac{\dfrac{a\sqrt{17}}{2}.\dfrac{a\sqrt{5}}{5}}{\sqrt{\bigg(\dfrac{a\sqrt{17}}{2}\bigg)^2+\bigg(\dfrac{a\sqrt{5}}{5}\bigg)^2}}$ $\Large =\dfrac{a\sqrt{1513}}{89}.$