Cho hình chóp S.ABCS.ABC có đáy là tam giác vuông tại AA v

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCS.ABC có đáy là tam giác vuông tại AA và ^ABC=30∘ˆABC=30∘ . Đỉnh SS cách đều các điểm A,B,CA,B,C. Biết khoảng cách từ SS đến mặt phẳng đáy bằng a√3a√3 , khoảng cách từ BB đến mặt phẳng (SAC)(SAC) bằng 2a√22a√2. Thể tích khối chóp đã cho bằng.
Đáp án án đúng là: B
Lời giải chi tiết:
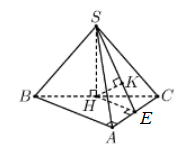
Gọi HH là trung điểm BCBC. Từ giả thiết suy ra SH⊥(ABC)→SH=a√3SH⊥(ABC)→SH=a√3
Ta có d(B;(SAC))=2d(H;(SAC))→d(H;(SAC))=a√2d(B;(SAC))=2d(H;(SAC))→d(H;(SAC))=a√2
Kẻ HE⊥AC(EHE⊥AC(E là trung điểm AC)AC), kẻ HK⊥SEHK⊥SE (1)
Ta có {AC⊥HEAC⊥SH ⇒AC⊥(SHE)⇒AC⊥HK (2)
Từ (1) và (2), suy ra HK⊥(SAC) nên HK=d(H;(SAC))=a√2
Trong tam giác vuông SHE, tính được HE=√6a⇒AB=2√6a^ABC=30∘→AC=2√2a
Diện tích tam giác S△ABC=12AB.AC=4√3a2
Vậy thể tích khối chóp VS.ABC=13S△ABC.SH=4a3
Đáp án B
Xem thêm các bài tiếp theo bên dưới