Cho hình chóp đều $\large S.ABCD$, đáy có cạnh bằng $\large a$. Gọi $\

Cho hình chóp đều $\large S.ABCD$, đáy có cạnh bằng $\large a$. Gọi $\large M, N$ lần lượt là trung điểm của $\large SA, SC$. Biết $\large (BM,DN)=60^{\circ}$. Gọi $\large h$ là chiều cao lớn nhất của hình chóp. Tính $\large h$

• A.

  A. $\large h=\dfrac{\sqrt{30}a}{2}$

• B.

  B. $\large h=\dfrac{\sqrt{30}a}{6}$

• C.

  C. $\large h=\dfrac{\sqrt{15}a}{2}$

• D.

  D. $\large h=\dfrac{\sqrt{42}a}{2}$

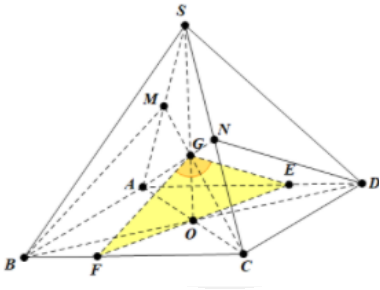
Gọi $\large O$ là tâm của hình vuông $\large ABCD$ và $\large G$ là trọng tâm tam giác $\large SAC$. Đường thẳng qua $\large G$ song song với $\large BM$ cắt $\large BC$ ở $\large F$.

Đường thẳng qua $\large G$ song song $\large DN$ cắt $\large AD$ tại $\large E$

Ta có $\large\dfrac{BF}{FC}=\dfrac{GM}{GC}=\dfrac{1}{2}=\dfrac{GN}{GA}=\dfrac{ED}{EA}\Rightarrow$ $\large\left\{\begin{align}EA=2ED\\ FC=2FB\end{align}\right.$

Suy ra $\large EF$ đi qua tâm của hình vuông $\large ABCD$ và $\large O$ là trung điểm của đoạn $\large EF$

Từ $\large\left ( BM;DN \right )=60^{\circ}\Rightarrow \left ( GE;GF \right )=60^{\circ}\Rightarrow$ $\large\left [\begin{align}\widehat{EGF}=60^{\circ}\\ \widehat{EGF}=120^{\circ}\end{align}\right.$

*) Với $\large\widehat{EGF}=60^{\circ}$

Ta có $\large\bigtriangleup GEF$ cân tại $\large G$, suy ra $\large\bigtriangleup GEF$ đều $\large GO=\frac{\sqrt{3}}{2}EF$

Hình vuông $\large ABCD$ có cạnh $\large a$ nên ta dễ dàng tính được $\large EF=\dfrac{\sqrt{10}a}{3}$

Suy ra chiều cao của chóp $\large SO=3GO=3\cdot \dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{10}}{3}a=\dfrac{\sqrt{30}a}{2}$

*) Với $\large\widehat{EGF}=120^{\circ}$

Ta có $\large\bigtriangleup GEF$ cân tại $\large G$ suy ra $\large GO=\dfrac{OF}{tan60^o}=\dfrac{EF}{2.tan60^o}=\dfrac{1}{2\sqrt{3}}EF=\dfrac{\sqrt{10}a}{6\sqrt{3}}\Rightarrow SO=3GO=\dfrac{\sqrt{30}a}{6}$

Do $\large\dfrac{\sqrt{30}a}{2}> \dfrac{\sqrt{30}a}{6}\Rightarrow h=\dfrac{\sqrt{30}a}{2}$

Đáp án A