Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45∘. Tính theo a khoảng cách h giữa hai đường thẳng SB,AC
Đáp án án đúng là: D
Lời giải chi tiết:
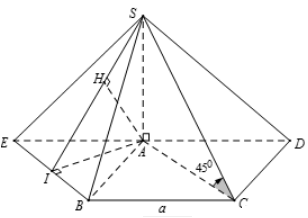
Ta có SA⊥(ABCD) ⇒(SC,(ABCD))=^SCA=450
Suy ra tam giác SAC vuông cân tại A
Dựng điểm E sao cho ACBE là hình bình hành, khi đó AC//EB⇒SA=AC=BE=a√2
⇒AC//(SBE)⇒d(AC;SB)=d(AC;(SBE))=d(A;(SBE)) (1)
Kẻ AI⊥EB(IϵEB), kẻ AH⊥SI(HϵSI)⇒d(A;(SBE))=AH (2)
Cách 1: Tam giác ABE vuông cân tại A⇒AI=EB2=AC2=a√2
Cách 2: Ta có AI=2SABEEB=SABCDAC=a2a√2=a√2
Xét tam giác SAI, ta có:
1AH2=1SA2+1AI2=12a2+2a2=52a2⇒AH=√10a5 (3)
Từ (1), (2), (3) suy ra
h=d(AC;SB)=√10a5
Đáp án D
Xem thêm các bài tiếp theo bên dưới