Cho lăng trụ $\large ABCD.A'B'C'D'$ có $\large A'.ABD$ là hình chóp đề

Cho lăng trụ $\large ABCD.A'B'C'D'$ có $\large A'.ABD$ là hình chóp đều, $\large AB=AA'=a$. Tính theo $\large a$ khoảng cách giữa hai đường thẳng $\large AB'$ và $\large A'C'$

• A.

  A. $\large\dfrac{a\sqrt{11}}{2}$

• B.

  B. $\large\dfrac{a\sqrt{22}}{22}$

• C.

  C. $\large\dfrac{a\sqrt{22}}{11}$

• D.

  D. $\large\dfrac{3a\sqrt{11}}{2}$

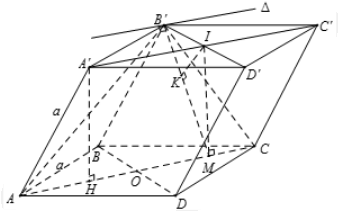
Gọi $\large H$ là trọng tâm tam giác $\large ABD$. Do $\large A'ABD$ là hình chóp đều nên $\large A'H\perp (ABD)$ hay $\large A'H\perp (ABCD)$

Tam giác $\large ABD$ đều cạnh $\large a$ nên $\large AH=\dfrac{a\sqrt{3}}{3}$ 

Khi đó $\large A'H=\sqrt{A'A^{2}-AH^{2}}=\sqrt{a^{2}-\dfrac{3a^{2}}{9}}=\dfrac{a\sqrt{6}}{3}$

Gọi $\large A'C'\cap B'D'=\left \{ I \right \}$ . Do $\large A'C'//AC\Rightarrow A'C'//(B'AC)\Rightarrow d(AB';A'C')=d(A'C';(B'AC))=d(I;(B'AC))$ (1)

Kẻ $\large IM\perp AC(M\epsilon AC)\Rightarrow IM//A'H\Rightarrow \left\{\begin{align}IM=A'H=\dfrac{a\sqrt{6}}{3}\\ IM\perp(A'B'C'D)\end{align}\right.$

Ta có: $\large (B'AC)\cap (A'B'C'D')=\bigtriangleup //A'C'\Rightarrow \bigtriangleup \perp IM$

Do $\large IB'\perp A'C'\Rightarrow IB'\perp \bigtriangleup \Rightarrow \bigtriangleup \perp (IB'M)$

Kẻ $\large IK\perp B'M(K\epsilon B'M)$

Khi đó $\large\Rightarrow d(I;B'AC)=IK$ (2)

Ta có $\large IB'=\dfrac{B'D'}{2}=\dfrac{BD}{2}=\dfrac{a}{2}$

Xét tam giác $\large IB'M$ ta có:

$\large\dfrac{1}{IK^{2}}=\dfrac{1}{IB'^{2}}+\dfrac{1}{IM^{2}}=\dfrac{4}{a^{2}}+\dfrac{3}{2a^{2}}=\dfrac{11}{2a^{2}}\Rightarrow IK=\dfrac{a\sqrt{22}}{11}$ (3)

Từ (1), (2), (3) suy ra:

$\large d(AB';A'C')=\dfrac{a\sqrt{22}}{11}$

Đáp án C