Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp

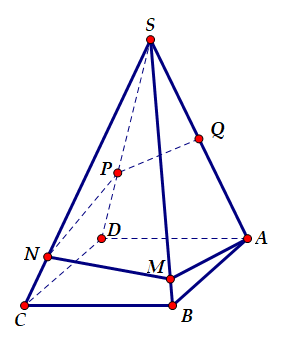
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn đèn hình tứ giác đều $\large S.ABCD$ cạnh bên $\large SA=600$ mét, $\large\widehat{ASB}=15^{\circ}$ . Do có sự cố đường dây diện tại điểm $\large Q$ (là trung điểm của $\large SA$) bị hỏng, người ta tạo ra một con đường từ $\large A$ đến $\large Q$ gồm bốn đoạn thẳng $\large AM, MN, NP, PQ$ (hình vẽ). Để tiết kiệm kinh phí, kĩ sư đã nghiên cứu và có được chiều dài con đường từ $\large A$ đến $\large Q$ ngắn nhất. Tính tỉ số $\large k=\dfrac{AM+MN}{NP+PQ}$

• A.

  A. 2

• B.

  B. $\large\dfrac{3}{2}$

• C.

  C.$\large\dfrac{4}{3}$

• D.

  D. $\large\dfrac{5}{2}$

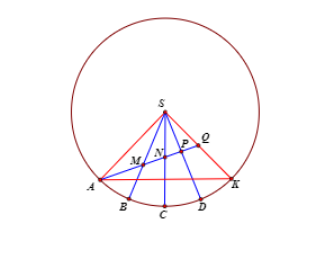
Giả sử trải các hình chóp đều trên đường tròn tâm $\large S$ và bán kính $\large R=SA$ ta được $\large\bigtriangleup SAK$ có $\large\widehat{ASB}=15^{\circ}\cdot 4=60^{\circ}\Rightarrow \bigtriangleup SAK$ đều.

Mà đoạn đường $\large AQ$ ngắn nhất khi $\large A,M,N,P,Q$ thẳng hàng. Khi đó $\large N$  là trọng tâm $\large \bigtriangleup SAK$

Suy ra $\large k=\dfrac{AM+MN}{NP+PQ}=\dfrac{AN}{NQ}=2$

Đáp án A