Cho hình chóp đều S.ABCS.ABC có SA=2a,AB=3aSA=2a,AB=3a. Tính tan
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp đều S.ABCS.ABC có SA=2a,AB=3aSA=2a,AB=3a. Tính tan của góc tạo bởi hai mặt phẳng (SBC)(SBC) và (ABC)(ABC)
Đáp án án đúng là: D
Lời giải chi tiết:
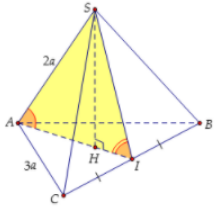
Gọi I là trọng tâm của tam giác ABC
Ta có: AH=23AI=23.3a√32=a√3AH=23AI=23.3a√32=a√3
Ta có: HI⊥BC⇒(^(SBC),(ABC))=^(SI,AI)=^(SIA)HI⊥BC⇒(ˆ(SBC),(ABC))=ˆ(SI,AI)=ˆ(SIA)
Ta có: {SH=√SA2−AH2=√(2a)2−(a√3)2HI=AH2=a√32 ⇒tan^SIA=SHIH=aa√32=2√33
Đáp án D