Cho hàm số y=f(x) xác định trên $\large \mathbb{R} \backslash(\pm 1\}$

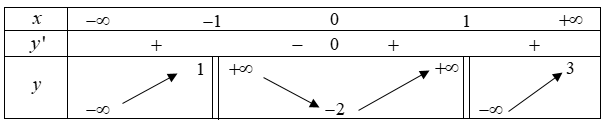
Cho hàm số y=f(x) xác định trên $\large \mathbb{R} \backslash(\pm 1\}$, liên tục trên mỗi khoảng xác định của nó và có bảng biến thiên như hình vẽ dưới đây

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f(x) là.

• A.

  A. 1

• B.

  B. 2

• C.

  C. 3

• D.

  D. 4

Chọn C

Theo bảng biến thiên của hàm số y=f(x) ta có:

Tiệm cận đứng:

Ta có $\large \lim _{x \rightarrow-1^{+}} f(x)=+\infty \Rightarrow$ hàm số y=f(x) có tiệm cận đứng x=-1.

$\large \lim _{x \rightarrow 1^{-}} f(x)=-\infty \Rightarrow$ hàm số y=f(x) có tiệm cận đứng x=1.

Vậy đồ thị hàm số có 2 tiệm cận đứng.

Tiệm cận ngang:

Ta có $\large \lim _{x \rightarrow +\infty} f(x)=3 \Rightarrow$ hàm số y=f(x) có tiệm cận ngang y=3.

Vậy đồ thị hàm số có 1 tiệm cận ngang.

Kết luận: Tổng tiệm cận đứng và ngang của đồ thị hàm số y=f(x)  là 3.